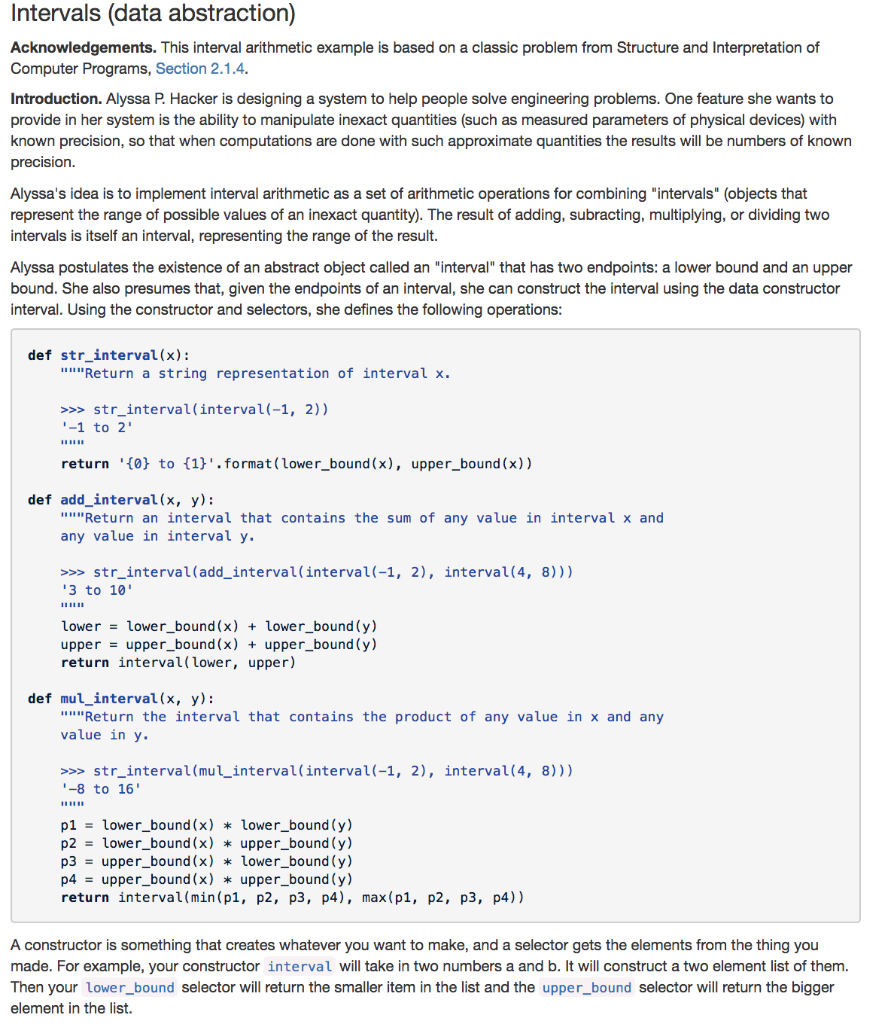
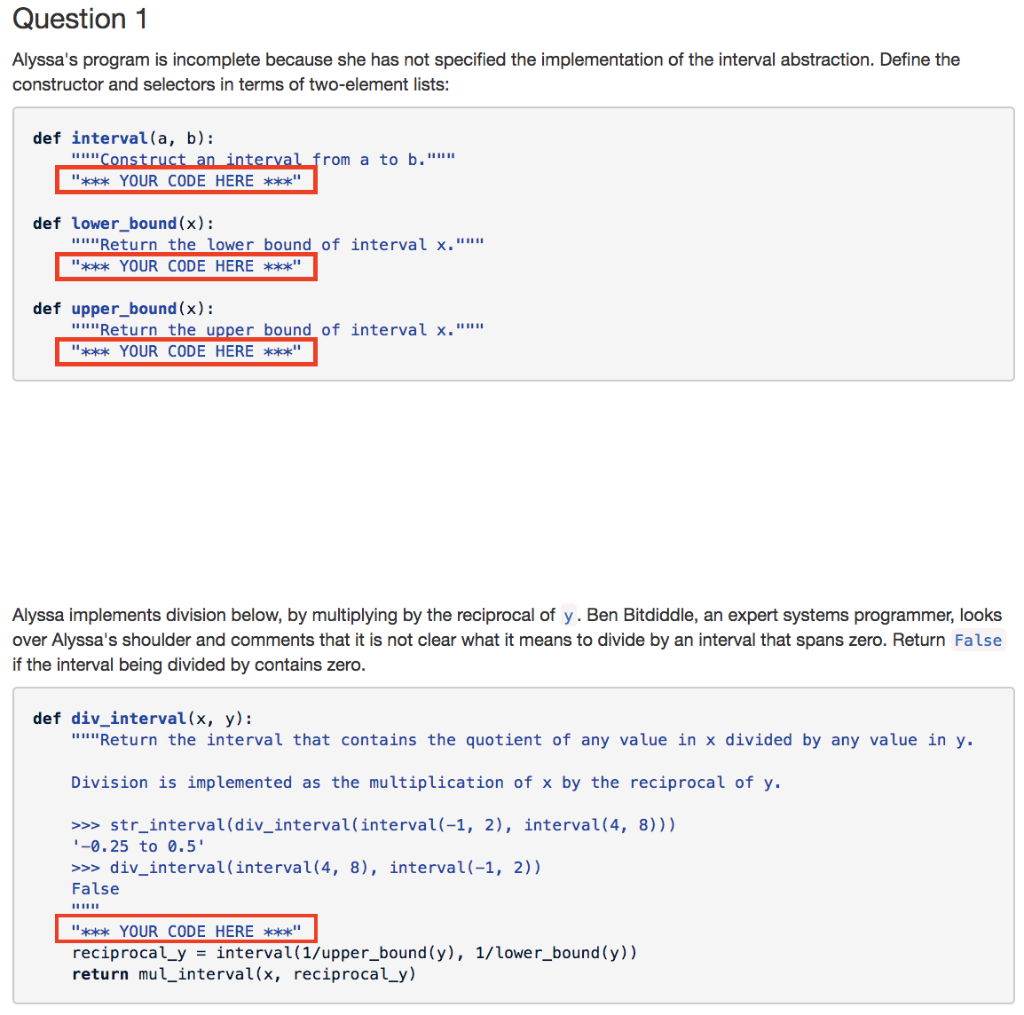
Intervals (data abstraction) Acknowledgements. This interval arithmetic example is based on a classic problem from Structure and Interpretation of Computer Programs, Section 2.1.4 Introduction. Alyssa P. Hacker is designing a system to help people solve engineering problems. One feature she wants to provide in her system is the ability to manipulate inexact quantities (such as measured parameters of physical devices) with known precision, so that when computations are done with such approximate quantities the results will be numbers of known precision. Alyssa's idea is to implement interval arithmetic as a set of arithmetic operations for combining "intervals" (objects that represent the range of possible values of an inexact quantity). The result of adding, subracting, multiplying, or dividing two intervals is itself an interval, representing the range of the result. Alyssa postulates the existence of an abstract object called an "interval" that has two endpoints: a lower bound and an upper bound. She also presumes that, given the endpoints of an interval, she can construct the interval using the data constructor interval. Using the constructor and selectors, she defines the following operations def str_interval (x) "Return a string representation of interval x. >>>str_interval (interval (-1, 2)) -1 to 2 return '0 to 1.format(lower_bound(x), upper_bound(x)) def add_interval(x, y): ""Return an interval that contains the sum of any value in interval x and any value in interval y. >>str_interval(add_interval(interval(-1, 2), interval(4, 8))) 3 to 10 lower lower_bound (x) lower_bound (y) upperupper_bound (x) upper_bound (y) return interval(lower, upper) def mul_interval(x, y): ""Return the interval that contains the product of any value in x and any va Lue in y str_interval(mul interval(interval(-1, 2), interval (4, 8))) -8 to 16 pllower_bound (x) lower_bound (y) p2-lower bound(x) * upper_bound (y) -upper_bound(x) lower_bound(y) p4 = upper-bound (x) * upper-bound (y) return interval(min(pl, p2, p3, p4), max(p1, p2, p3, p4)) A constructor is something that creates whatever you want to make, and a selector gets the elements from the thing you made. For example, your constructor interval will take in two numbers a and b. It will construct a two element list of them. Then your lower_bound selector will return the smaller item in the list and the upper_bound selector will return the bigger element in the list. Question 1 Alyssa's program is incomplete because she has not specified the implementation of the interval abstraction. Define the constructor and selectors in terms of two-element lists: def interval (a, b): rom a to b." "YOUR CODE HERE def lower_bound(x): "'Return the lower bound of interval x."" YOUR CODE HERE" def upper_bound(x): "Return the upper bound of interval x." YOUR CODE HERE " Alyssa implements division below, by multiplying by the reciprocal of y. Ben Bitdiddle, an expert systems programmer, looks over Alyssa's shoulder and comments that it is not clear what it means to divide by an interval that spans zero. Return False if the interval being divided by contains zero def div_interval(x, y): "Return the interval that contains the quotient of any value in x divided by any value in y. Division is impLemented as the multiplication of x by the reciprocal of y >>str interval (div_interval(interval(-1, 2), interval (4, 8))) "-0.25 to 0.5 >>>div_interval(interval (4, 8), interval(-1, 2)) False YOUR CODE HERE reciprocal_y-interval(1/upper_bound (y), 1/lower_bound(y)) return mul_interval(x, reciprocal_y)