Intro

Consider a $5-$year credit default swap with annual payments and a notional principal of $\backslash (\backslash$$ $30,000,000\backslash ).$ Assume that defaults can happen only halfway through each year. The hazard rate is $\backslash (2\backslash \%\backslash )$ with continuous compounding and the recovery rate is $60\backslash \%.$

The risk$-$free rate is $\backslash (2\backslash \%\backslash )$ with continuous compounding, for all maturities.

Part $1$

Attempt $\backslash (2/3\backslash )$ for $9\mathrm{.}5$ pts$.$

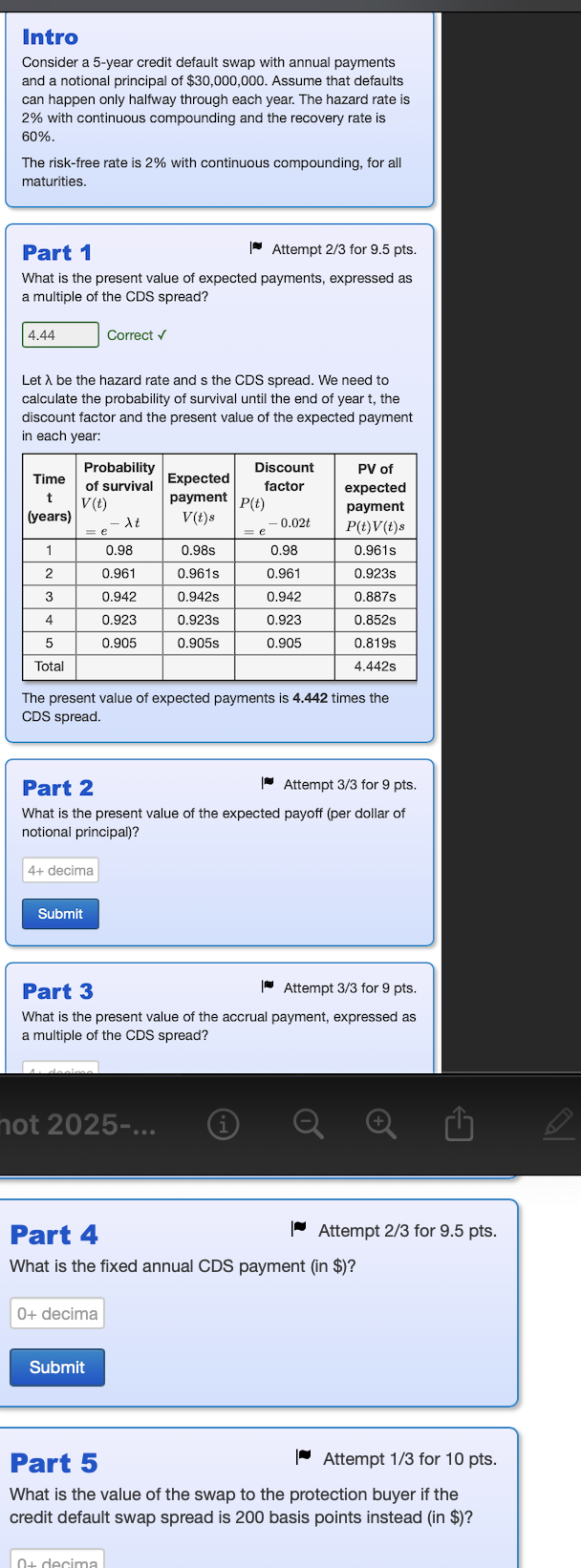
What is the present value of expected payments, expressed as a multiple of the CDS spread? Correct $\backslash (\backslash$checkmark $\backslash )$

Let $\backslash (\backslash$lambda $\backslash )$ be the hazard rate and $\backslash ($ s $\backslash )$ the CDS spread. We need to calculate the probability of survival until the end of year t $,$ the discount factor and the present value of the expected payment in each year:Time t $($years$)$Probability of survival $\backslash ($ V$($t$)\backslash )\backslash (=$e$^\{-\backslash$lambda t$\}\backslash )$Expected payment $\backslash ($ V$($t$)$ s $\backslash )$Discount factor $\backslash ($ P$($t$)\backslash )\backslash (=$e$^\{-0\mathrm{.}02$ t$\}\backslash )$PV of expected payment $\backslash ($ P$($t$)$ V$($t$)$ s $\backslash )$

The present value of expected payments is $4\mathrm{.}442$ times the CDS spread.

Part $2$

Attempt $\backslash (3/3\backslash )$ for $9$ pts$.$

What is the present value of the expected payoff $($per dollar of notional principal$)?$

What is the present value of the accrual payment, expressed as a multiple of the CDS spread?

Part $4$

Attempt $\backslash (2/3\backslash )$ for $9\mathrm{.}5$ pts$.$

What is the fixed annual CDS payment $($in $\backslash$$$)?$

What is the value of the swap to the protection buyer if the credit default swap spread is $200$ basis points instead $($in $\backslash$$$)?$