Question: Intro to discrete math We define ~ as on the SCC graph: 8= {(v, v') E V/ | In EN, 3vo, . .., Un

Intro to discrete math

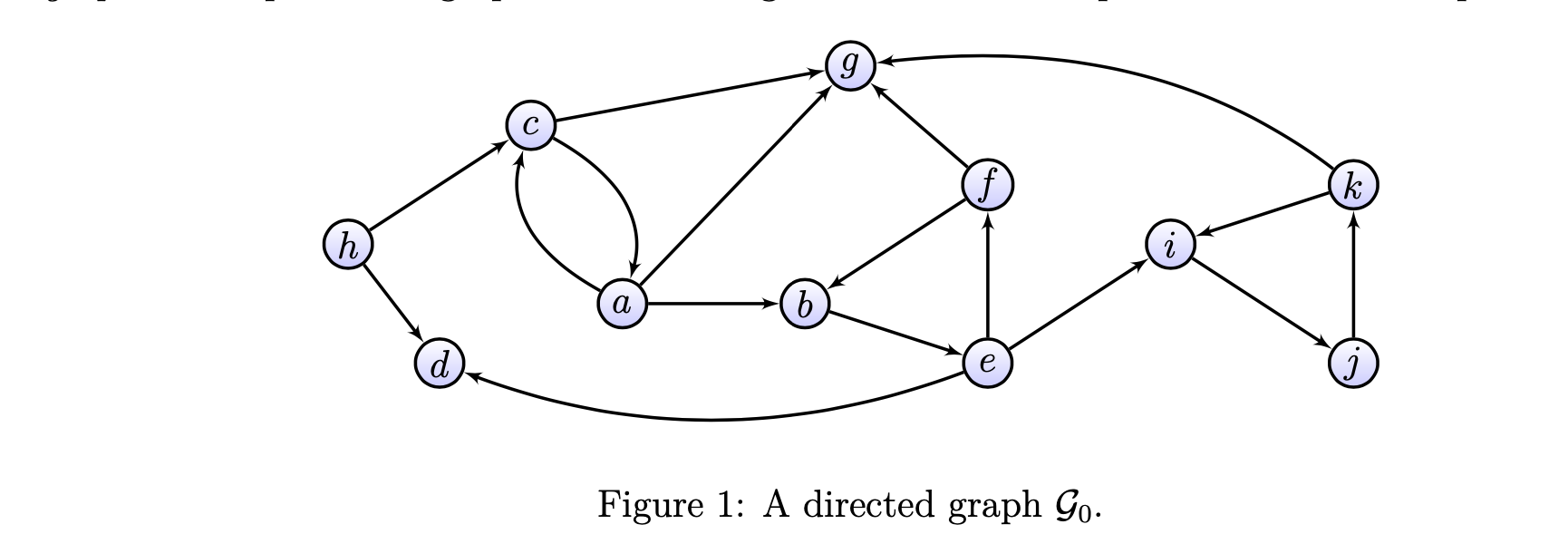
We define ~ as " on the SCC graph": 8= {(v, v') E V/ | In EN, 3vo, . .., Un EV/s, V0 = VAUn = VAVie {1, ..., n}, (vi-1, vi) ET/}. Exercise 6. Answer the following questions, each time proving your claim: 1. Is reflexive? 2. Is ~ symmetric? 3. Is ~antisymmetric? Hint: Prove the following lemma: Lemma. For any vertices [vo, [U']s E V/s, if [ulo ~ ['l then v v. 4. Is ~ transitive? 5. Is an equivalence relation? 6. Is an order relation? If yes, is it total? Note: In this exercise we consider ~ not over a particular graph, but in general. So when the answer is yes, a proof must be for any graph, but when the answer is no, a counterexample can be from a particular graph (from Go/ for instance).\f

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

discrete math Directed Graphs Let us first give the formal definition: Definition (Directed graph). A directed graph is given by a set of vertices V and a transition relation T C V x V. We write 9 =...

My question is number 50. This is an intro to discrete math course. please give a detailed answer thank you so much! 2.2 Set operations 13 49. Let Ai be the set of all nonempty bit strings (that is,...

Intro. To discrete Math Using the rules of propositional calculus, prove that ((P 9) p)^-p is a contradiction. Indicate at each step what rule was used

Intro To discrete Math Denition (Directed graph). A directed graph 'is given by a set of vertices V and a transition relation T Q V X V. We write g = (V, T). Behind this somewhat abstract denition,...

My course is an intro to discrete math so I wasnt sure where to post. Please give a step by step answer. Thanks! 6. Prove that if 3m 2is odd, then so is n

Need Help with these two questions. Intro to Discrete Math - Coen 231 2. Let A be a 5x3 matrix, B be a 4x3 matrix, and C be a 3x4 matrix. Determine which of the following products are defined, and...

Intro to discrete math Let 2 {(0,12') E V x V I P(v, s\") A PCs", :0}. We will use an inx notation for this relation and write 1) if instead of (v, 12') IE @. Exercise 4. 1. Describe relation 93 in...

Intro To discrete math \fLet -> = {(v,v') E V x V | P(v, v')}. We will use an inx notation for this relation and write 1} w 11' instead of (11,11') 6w. We also write 1} 71+ 11' instead of (v,v') 9}...

Program the following: We will use a double adjacency list graph to represent courses and their prerequisites: Each vertex represents course information Edges represent prerequisite relationships...

NO ARRAYS and NO SYS.OUT onlu use JOP please help!!! You have been hired by a University to create and manage their course registration portal. The university is offering six IT courses in Fall 2023....

In a pilot study examining the effectiveness of three commercials (A. B. and C), 10 consumers were assigned to view each commercial and rate it on a 9-point Likert scale, flic data obtained from the...

The panel shown forms the end of a trough which is filled with water to the line AA′. Referring to Sec. 9.2, determine the depth of the point of application of the resultant of the hydrostatic...

. 1 5 2 0 1 5 0 . 5 The conflict of ranking based on IRR and NPV is due to: Cash flow currency Project shareholders Project management Cash flow size . 1 5 2 0

Shares may be issued at a price which is termed as: at par; at a premium; and at a discount . What is the meaning of these concepts?