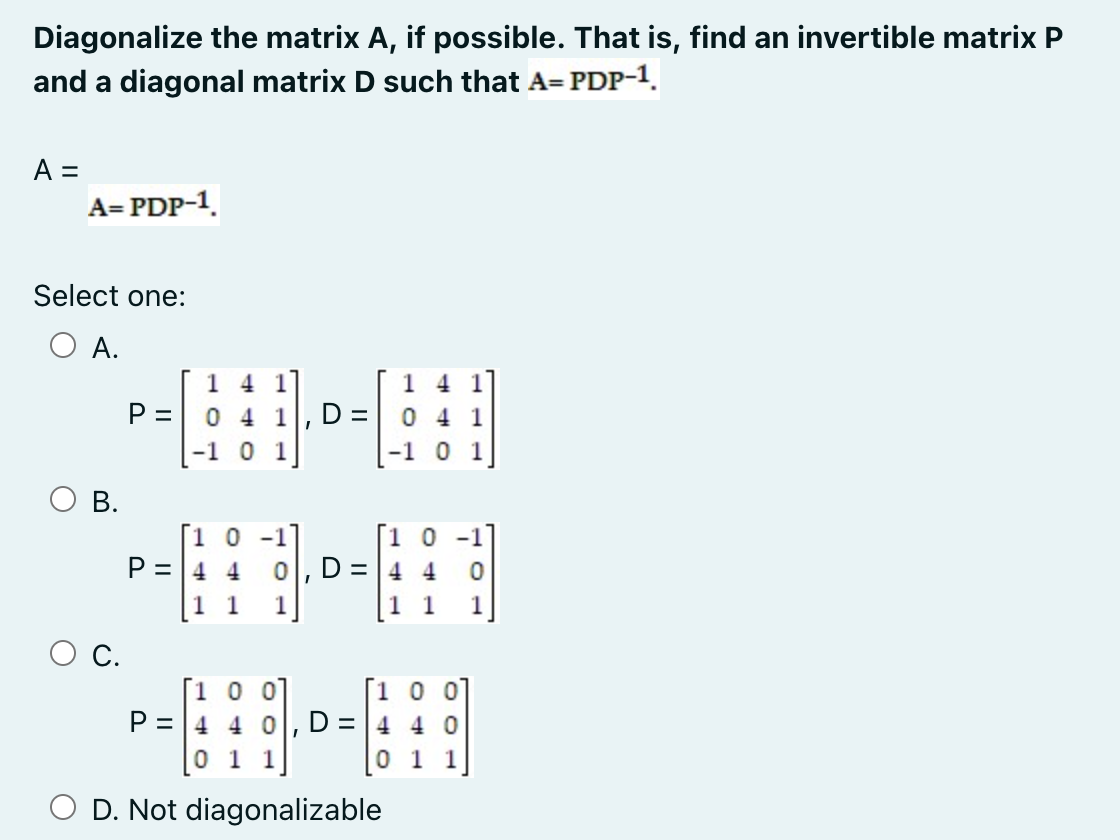
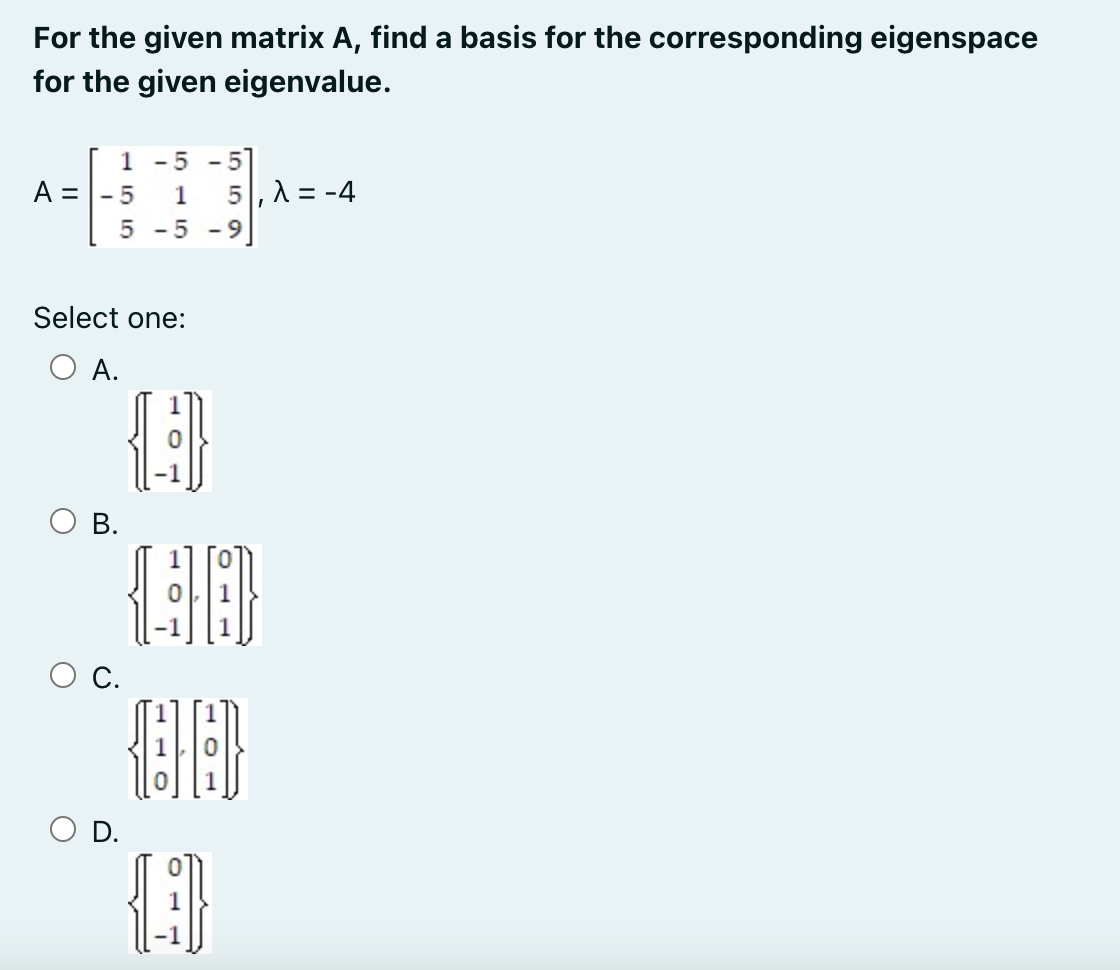
Question: Intro to Linear Algebra - Chapter 5: Similarity Diagonalize the matrix A, if possible. That is, find an invertible matrix P and a diagonal matrix
Intro to Linear Algebra - Chapter 5: Similarity
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock