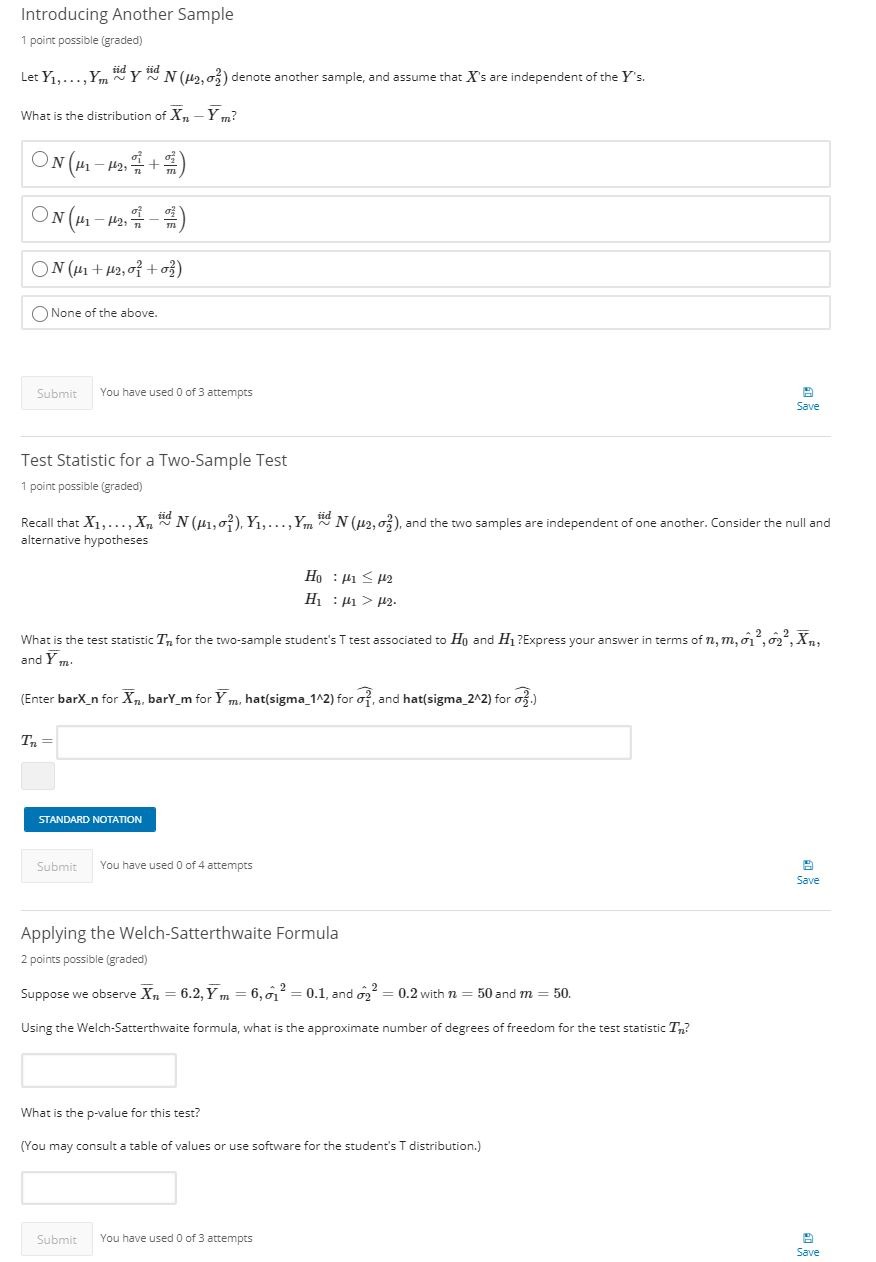
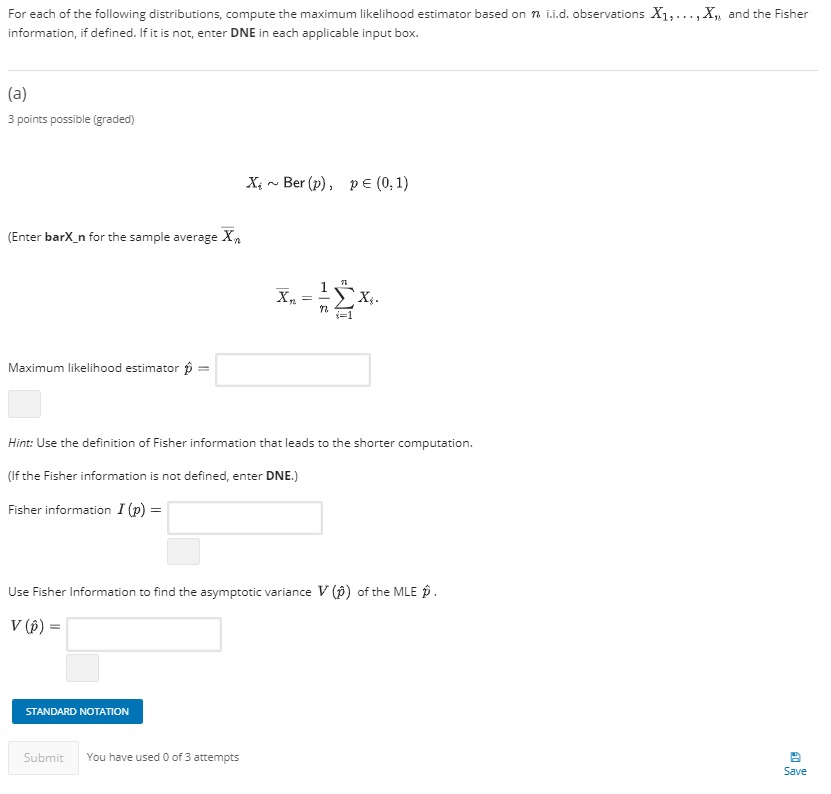
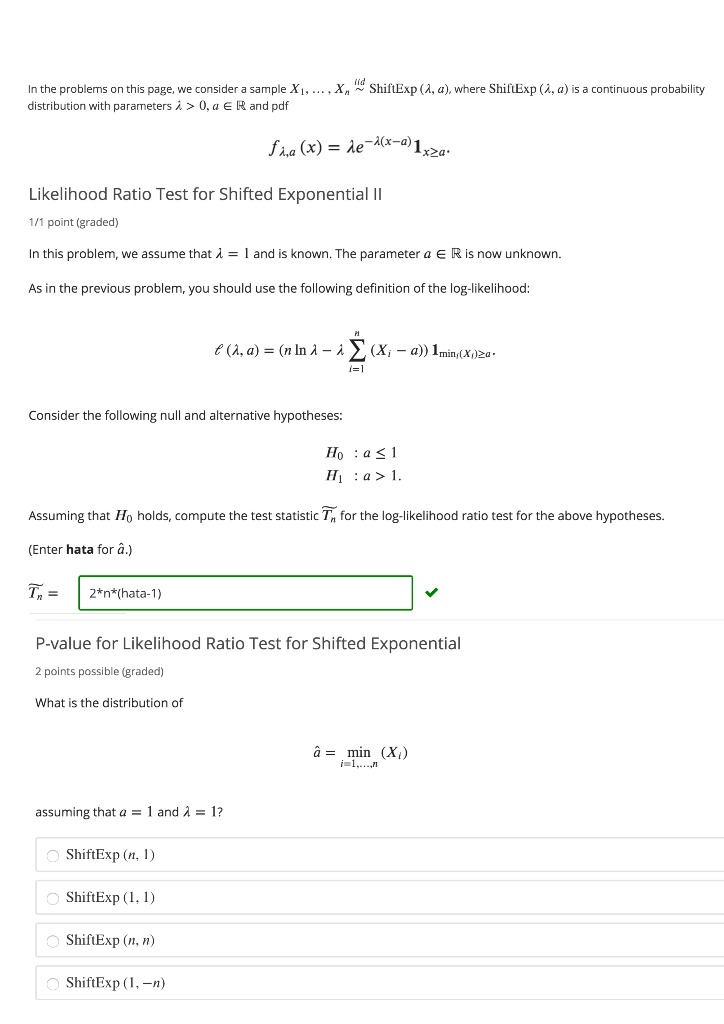
Introducing Another Sample 1 point possible (graded) Let Y1, . .., Ym " Y " N (12, 0;) denote another sample, and assume that X's are independent of the Y's. What is the distribution of X, - Y m? ON( M - 12, +) ON( 1 - 12, - - ON ( #1 + 12, 07 + 03) None of the above. Submit You have used 0 of 3 attempts Save Test Statistic for a Two-Sample Test 1 point possible (graded) Recall that X1, . .., Xn "" N (#1, ;), Yl,..., Ym "N (#2, 0;), and the two samples are independent of one another. Consider the null and alternative hypotheses Ho : #1 5 #2 HI : #1 > #2- What is the test statistic T'" for the two-sample student's T test associated to Ho and Hi ?Express your answer in terms of n, m, 61 , 62 , Xn, and Y m. (Enter bark n for Xn, barY_m for Y m, hat(sigma_142) for of, and hat(sigma_212) for ?.) Th = STANDARD NOTATION Submit You have used 0 of 4 attempts Save Applying the Welch-Satterthwaite Formula 2 points possible (graded) Suppose we observe Xn = 6.2, Ym = 6,01 = 0.1, and 02- = 0.2 with n = 50 and m = 50. Using the Welch-Satterthwaite formula, what is the approximate number of degrees of freedom for the test statistic In? What is the p-value for this test? (You may consult a table of values or use software for the student's T distribution.) Submit You have used 0 of 3 attempts CaveFor each of the following distributions, compute the maximum likelihood estimator based on n i.i.d. observations X1; ..., X, and the Fisher information, if defined. If it is not, enter DNE in each applicable input box. (a) 3 points possible (graded) Xi ~ Ber (p), DE (0, 1) (Enter barX_n for the sample average X, Xn. = = Maximum likelihood estimator p = Hint: Use the definition of Fisher information that leads to the shorter computation. (If the Fisher information is not defined, enter DNE.) Fisher information I (p) = Use Fisher Information to find the asymptotic variance V (p) of the MLE p. V (p) = STANDARD NOTATION Submit You have used 0 of 3 attempts SaveIn the problems on this page, we consider a sample X1, .... X, ~ ShiftExp (1, a), where ShiftExp (1, a) is a continuous probability distribution with parameters > > 0, a E I and pdf faa (x) = de-1(x-@)1xza. Likelihood Ratio Test for Shifted Exponential II 1/1 point (graded) In this problem, we assume that 1 = 1 and is known. The parameter a E R is now unknown. As in the previous problem, you should use the following definition of the log-likelihood: f (1, a) = (nina - A > (X; - a)) 1min (X,)24- 1= 1 Consider the following null and alternative hypotheses: Ho : as1 H1 :a>1. Assuming that Ho holds, compute the test statistic 7, for the log-likelihood ratio test for the above hypotheses. (Enter hata for a.) In = 2*n*(hata-1) P-value for Likelihood Ratio Test for Shifted Exponential 2 points possible (graded) What is the distribution of a = min (X/) 1 1.....7 assuming that a = 1 and 1 = 1? ShiftExp (n, 1) O ShiftExp (1, 1) O ShiftExp (n, n) O ShiftExp (1, -m)