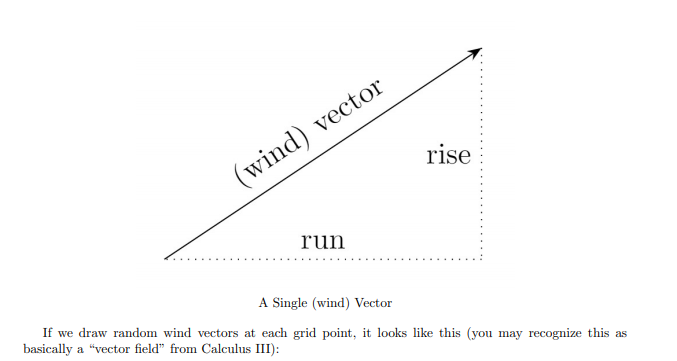
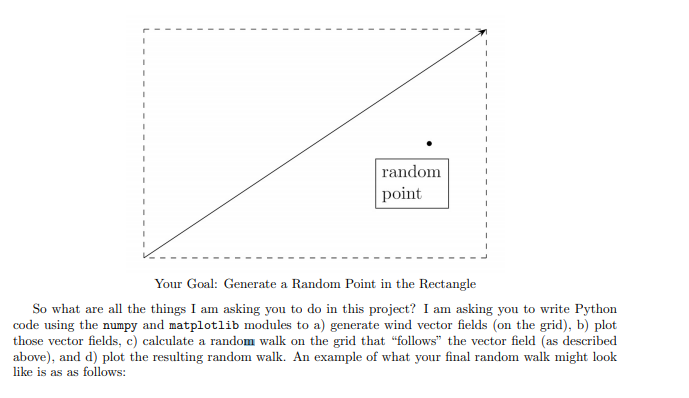
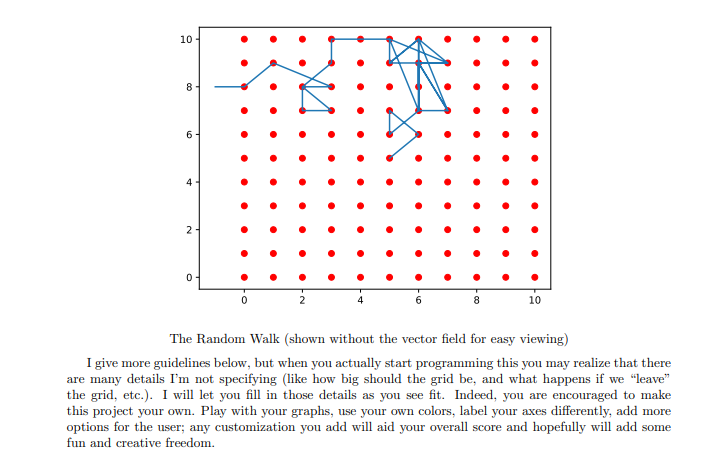
INTRODUCTION Random walks are a well-established concept with many variations and in this project I'd like you to simulate a particular type of random walk of our own design and I'd like you to graph it as best you can using matplotlib. In a basic random walk, a "person" starts somewhere on the integer grid in the ry-plane and moves one unit either up, down, left, or right randomly with equal probability. Tracking this walkers's motion along the grid of possible positions results in some very interesting graphs (see the wikipedia page for random walks) and is seen as a general model for certain types of random behavior. If you've never seen random walks before, please look them up on the internet before proceeding. A "typical" random walk on a grid might look like this: 10 8 2 0 0 6 10 Suppose that the person in the random walk does not move with complete randomness, but instead roughly follows some predetermined directions. Imagine that the person is being pushed along by the wind, say. Now, wind does not always blow straight in one direction, but might blow in different directions at different points in space. To represent this, let's think of wind as a vector at each point in space. You remember vectors, right? A vector is defined by its run and its rise (these can be positive or negative). rise (wind) vector run A Single (wind) Vector If we draw random wind vectors at each grid point, it looks like this (you may recognize this as basically a "vector field from Calculus III): 10 - 8 2 0 2 6 8 10 A Vector Field (of wind vectors) Now imagine that the walker is at a specific grid point in space and that point has a wind vector. The way one step of our random walk should work is that you should generate a random point in the rectangle that encloses the wind vector (see image below), and the grid point closest to that random point will be the one the random walker goes to. Note that the closest grid point might be the starting grid point or it might be a very far away grid point. In this way the random walk is still random but roughly follows the wind vector field at each step. EXAMPLE: If the walker is at (4,5) and the wind is blowing with vector (-1,3), then we should generate a random point in the rectangle given by 3