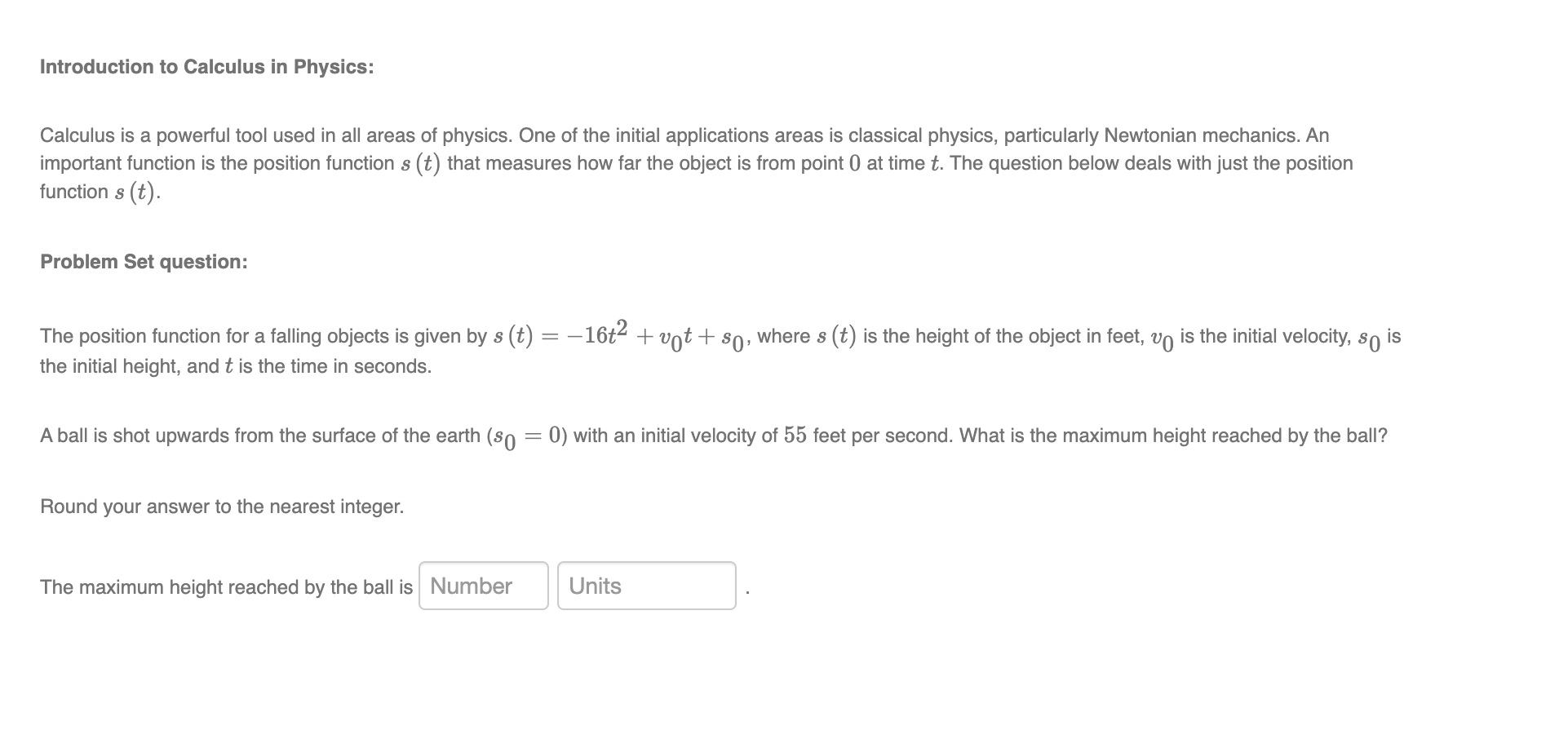
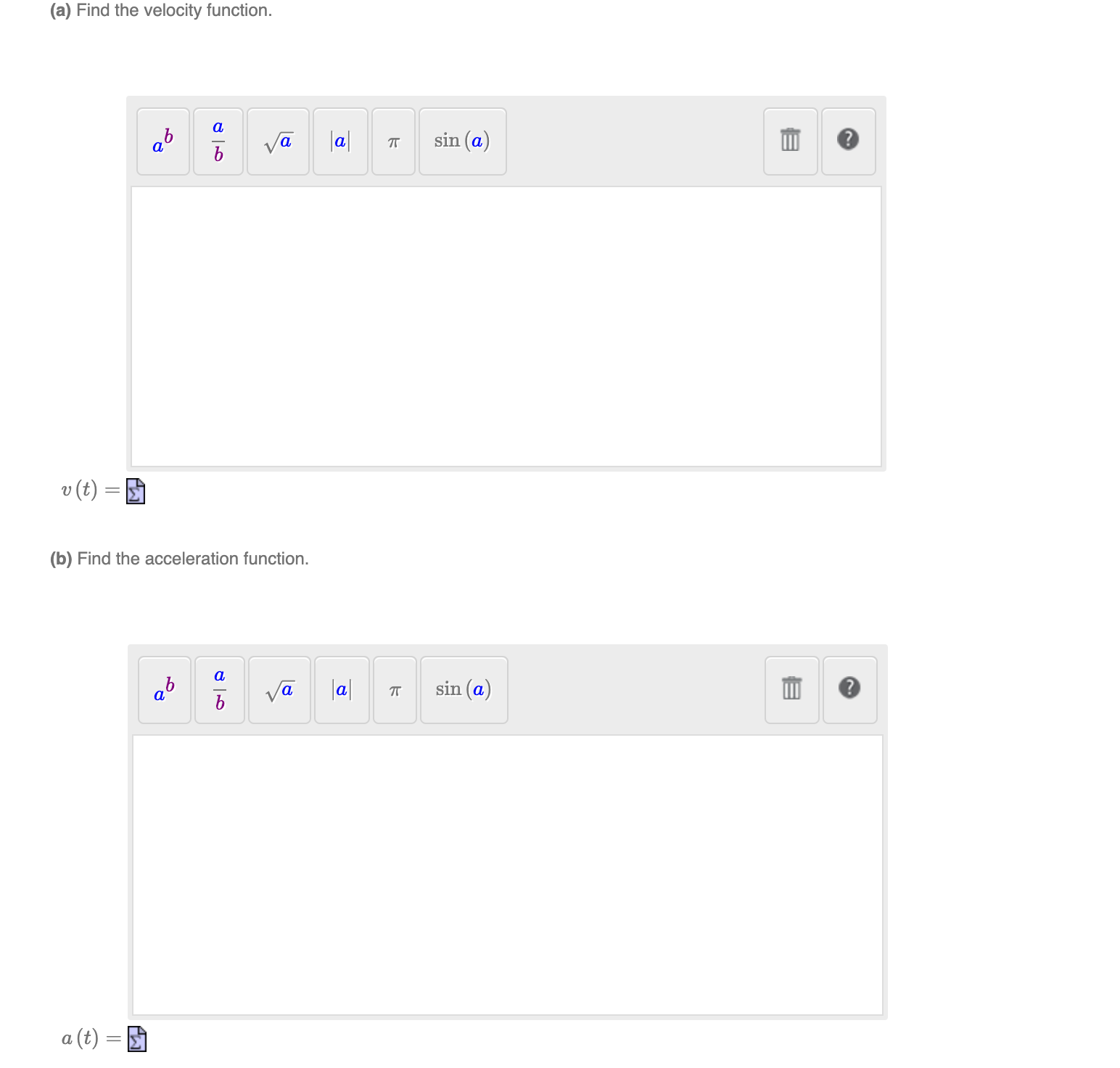
Introduction to Calculus in Physics: Calculus is a powerful tool used in all areas of physics. One of the initial applications areas is classical physics, particularly Newtonian mechanics. An important function is the position function .9 (t) that measures how far the object is from point 0 at time t. The question below deals with just the position function 5 (15). Problem Set question: The position function for a falling objects is given by s (t) = 16t2 + pot + 30, where .9 (t) is the height of the object in feet, 110 is the initial velocity, 50 is the initial height, and t is the time in seconds. A ball is shot upwards from the surface of the earth (.9 = 0) with an initial velocity of 55 feet per second. What is the maximum height reached by the ball? 0 Round your answer to the nearest integer. The maximum height reached by the ball is . In the previous Problem Set question, we started looking at the position function 5 (t), the position of an object at time t . Two important physics concepts are the velocity and the acceleration. If the current position of the object at time t is .9 (t), then the position at time h later is s (t + h). The average velocity (speed) during that additional time s t h s t his ((+'1( . If we want to analyze the instantaneous velocity at time 25, this can be made into a mathematical model by taking the limit as h ) 0, Le. the derivative 5' (t). Use this function in the model below for the velocity function 1) (t). The acceleration is the rate of change of velocity, so using the same logic, the acceleration function a (t) can be modeled with the derivative of the velocity function, or the second derivative of the position function a, (t) = 11' (t) = s" (25). Problem Set question: A particle moves according to the position function .9 (t) = ezt sin (5t). Enclose arguments of functions in parentheses. For example, sin (2t). (it) Find the velocity function.