Inverting intervals, Wilson interval, Jeffreys interval

• Assume that X follows a Binom (n, p) distribution with the parameters n known and p unknown.

I want a 100(1 - ??? ) % confidence interval for p.

The standard textbook interval is the large-sample interval

?CIs?=p^?z2????SE^(p^?)? ,

where ?p^?=nX?? is the sample proportion of successes,

?SE^(p^?)=np^?(1?p^?)??? is the estimated standard error of ?p^?? ,

?z2???? is the 100(1 - ?2??? ) th percentile of a standard normal distribution.

(a) Show that ?CIs?? is obtained by inverting the acceptance region of the large-sample level ??? test of ?H0?:p=p0?? vs ?H1?:p?=p0?? using the test statistic ?SE^(p^?)(p^??p)?? .

(b) Show that ?CIs?? , Wilson interval, can be obtained by using the null standard error ?np0?(1?p0?)??? in place of the estimated standard error used in the test statistic in part (a).

Show that the resulting interval is

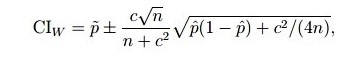
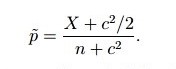
\f\f