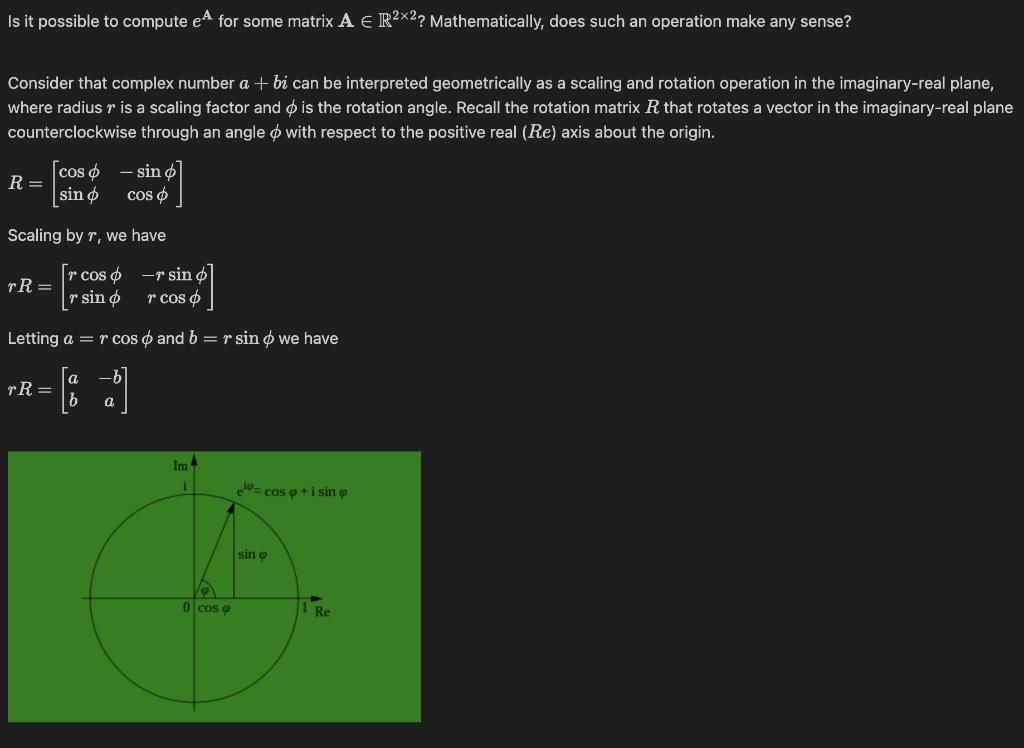
Is it possible to compute e for some matrix A E Rx2? Mathematically, does such an operation make any sense? Consider that complex number a + bi can be interpreted geometrically as a scaling and rotation operation in the imaginary-real plane, where radius r is a scaling factor and is the rotation angle. Recall the rotation matrix R that rotates a vector in the imaginary-real plane counterclockwise through an angle with respect to the positive real (Re) axis about the origin. cos o sin o Scaling by r, we have R = - sin cos r cos o r sin p Letting a = r cos [9] a rR= rR= -r sin r cos o and b = r sin o we have Im 0 cose e= cos o + i sin o sin o Re From Euler's formula, ei = cos + i sin , we can express ei as e with A=[5] 0 Now recall the Maclaurin series for the exponential function e is x=0 ml Maclaurin series to approximate e"? What will we find? = 1+x+ = N8 + What if we substitute A into the Write a Python program to approximate the matrix representation of e*. Use NumPy methods to compute powers of A in the Maclaurin series. In your program, use a while iterative construct to continue accumulating terms in the series until the approximation does not change between the approximation with N terms and N + 1 terms. If you denote the approximation with N terms as SN and the approximation with N + 1 terms as SN+1, you can stop iterating if the matrix norm ||SN+ SN ||2 < T for some small 7, for example, 10-7.