Question: is my solution correct? If not, How do I solve it? 4. (242=4 marks/ Let f () = isin (2). J' = in() + *

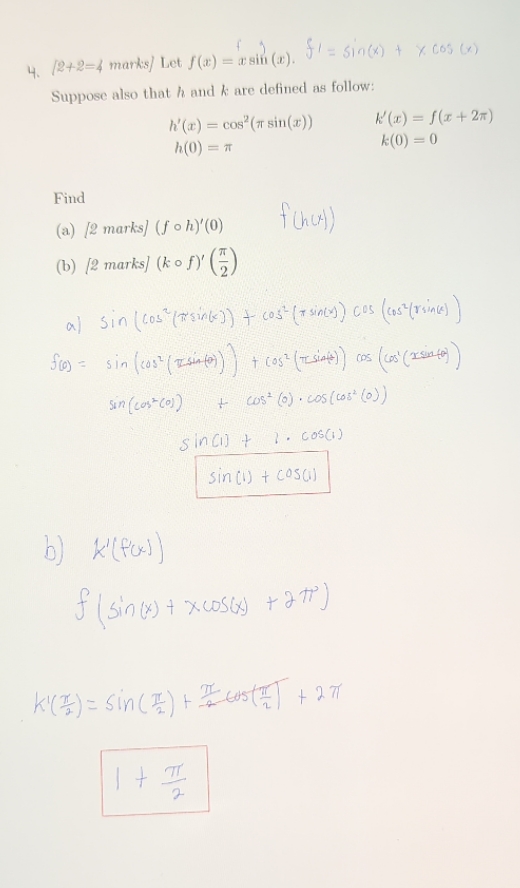
is my solution correct? If not, How do I solve it?

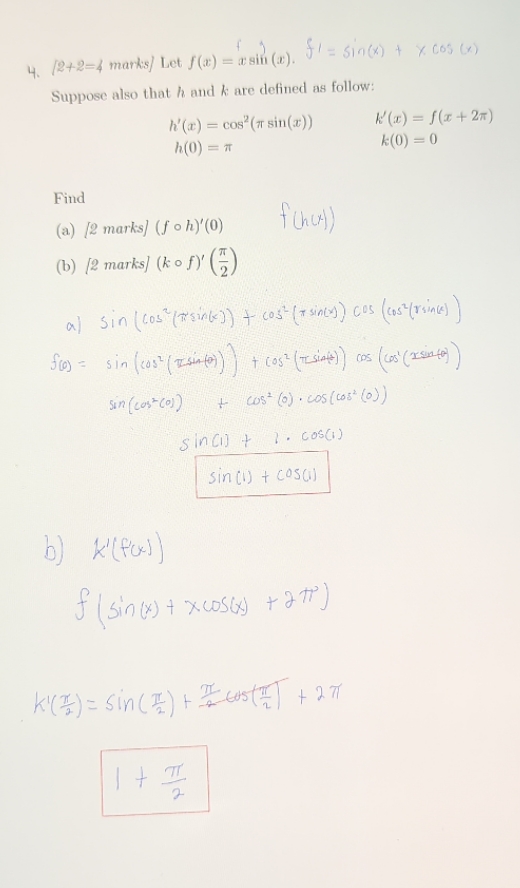
4. (242=4 marks/ Let f () = isin (2). J' = in() + * cos (x) Suppose also that h and & are defined as follow: h'(r) = cos' (i sin(2)) h(0) = k(0) = 0 Find (a) [2 marks] (f oh)'(0) ( b ) [2 marks) ( ko f )' ( ?) al Sin ( cos ( T'sink] ) + cost ( + since) cos (cost ( rsince) ) flo) = sin ( cost ( Isinto) ) ) + cos? ( Tsiaft) ) cos ( cost ( x- since to)) sin (costco) ) + cost (0) . cos ( cost (0) ) sindij + 1. cos() sin () + cosa) b) *' ( fox) ) f ( sin ( x) + xcos() + 271 ) KI ( #! ) = Sin ( I ) + # 60s(= ] + 271

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

How do I solve this? 4. (2+2=4 marks/ Let /(x) = rsin (x). Suppose also that h and & are defined as follow: h'(x) = cos (n sin(x)) k'(x) = f(x + 27) h(0) = k(0) = 0 Find (a) [2 marks) (f oh)'(0) (b)...

t = 1 i need it in 2-3 hours. please be quick. solve all the parts in short answer too no problem 4. [40 MARKS] Let t be the '7'\"1 digit of your Student ID. A consumer has a preference relation...

t=0 plz 4. [40 MARKS] Let t be the 7\" digit of your Student ID. A consumer has a preference relation defined by the utility function u(:c,y) = (t l 1 33)2 (t + 1 y)2. He has an income of w > 0 and...

(a) How does the use of condition codes complicate the implementation of a superscalar processor that supports out-of-order execution? [4 marks] (b) A branch predictor with a high prediction accuracy...

Math 2412 - Final Exam Review Problems 36. Write 7 [cos (? ) + isin (3)] in rectangular form. 37. Given 21 = 3 [cos () + isin ()] and z2 = 8 [cos () + isin ()], find z1 . 22. Write your answer in...

Problem 1 (100 marks) Liberty Taxes is a Vancouver based firm specializing in preparing Canadian Income Tax forms for their individual and corporate clients. Liberty processes only two types of...

Exercise Set 6.1: Sum and Difference Formulas Simplify each of the following expressions. 1. sin ( x ) 2. 3 cos x + 2 3. cos x 2 4. sin ( + x ) 5. sin 60 + sin 60 + 6. cos 60 + cos 60 + 7. cos x +...

Consider the trigonometric series a0 2 + X r=1 (ar cos rx + br sin rx) where a0, a1, a2, . . . and b1, b2, . . . are constants and suppose that f(x) is a periodic function of x with period 2. (a)...

A discrete sequence {xn} can be converted into a continuous representation x(t) = ts X n= (t n ts) xn, where ts is the sampling period. (a) State two characteristic properties of Dirac's function. [2...

Briefly describe ASCII and Unicode and draw attention to any relationship between them. [3 marks] (b) Briefly explain what a Reader is in the context of reading characters from data. [3 marks] A...

Foot and balance the T accounts prepared in Exercise 3-5A if necessary. Exercise 3-5A Sheryl Hansen started a business on May 1, 20--. Analyze the following transactions for the first month of...

How can liquidity and interest rate risk management objectives conflict in a DI? Where possible, provide examples. Are these conflicts resolvable? Explain.

Seasonal Products Corporation expects the following monthly sales: \ table [ [ January , $ 2 0 , 0 0 0 , July,$ 1 0 , 0 0 0 Show all images Show all images Show all images done loading

The force constant of a massless spring is 2 5 . 0 N / m . A mass of 0 . 4 5 kg is oscillating in simple harmonic motion at the end of the spring

The SBA loan program that slashed paperwork and approval time is the _____________ program.

What are the differences between efficiency and effectiveness? Why are Fayol's managerial functions an incomplete description of how organizations pursue these goals?

What is an organization? Why do people become members of organizations? Think of some organizations to which you belong. Why did you join these organizations? Think of an organization of which you...