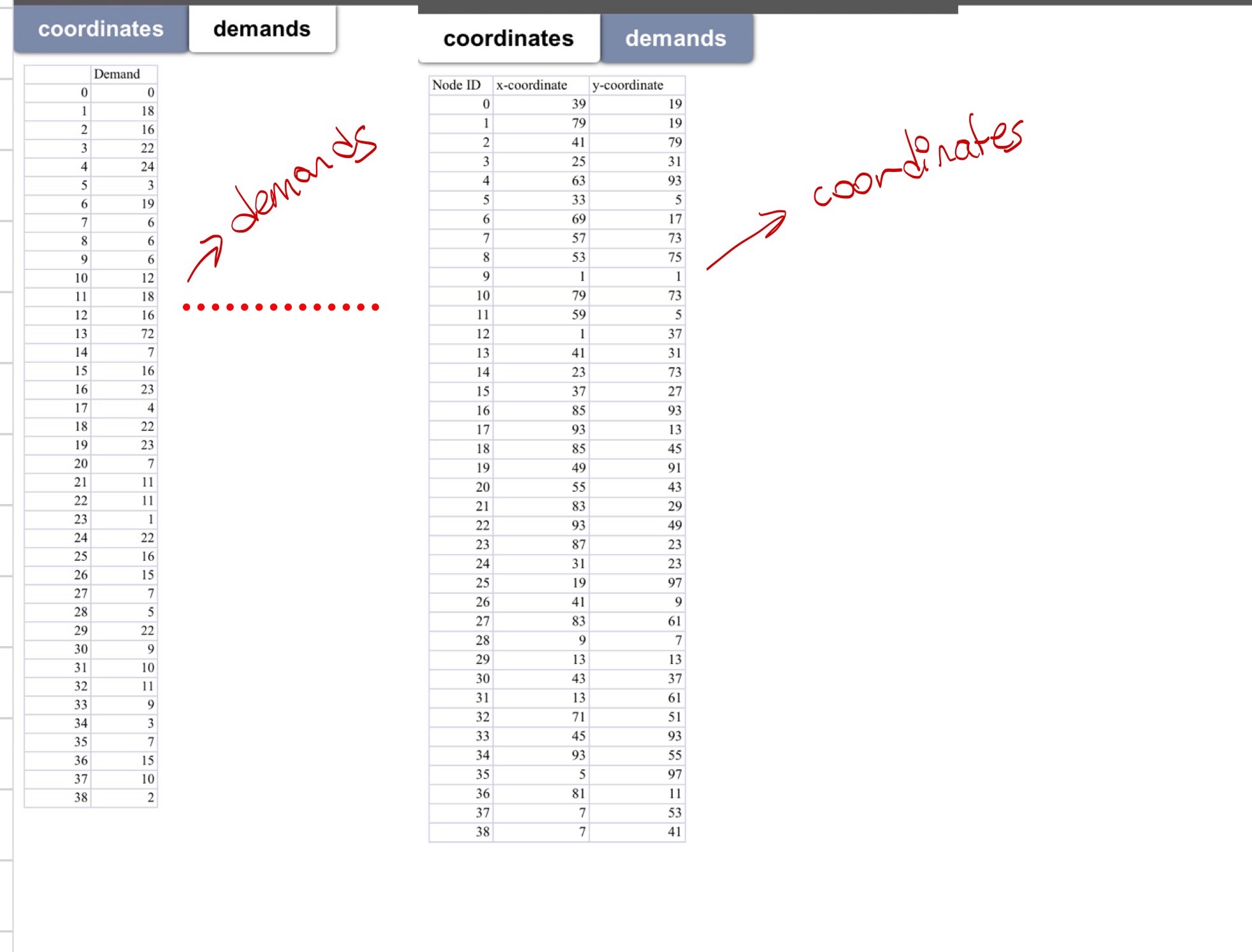
ISE $316$ Project $3$ December $2024$A delivery company serves $38$ customers daily. As an industrial engineer working in thiscompany, your task is to find the best routes to minimize the total transportation costs withhomogeneous fleet where each vehicle can carry $100$ units. Determine the minimum number ofvehicles based on that. $0$ shows the depot. You can find the coordinates and the demands in thegiven file. Ensure that the distance matrix is Euclidean. To solve the problem, you need tofollow the steps given below:a$.$ Apply Cluster First Route Second algorithms.b$.$ Implement Route First Cluster Second algorithms.These two parts are open where you can apply many different combination of construction andimprovement heuristics. For instance, this is a combination: Construction Algorithm x $+$Improvement Algorithm y$.$ The detailed instructions are given below:$1.$ In part a$,$ apply $2$ construction algorithms. Then, apply one of the improvementalgorithms over the resulting tour from the construction phase. So$,$ files will be like:Construction x $+$ Improvement y$2.$ In part b$,$ the followings are required:a$.$ Use Cheapest Insertion algorithm at construction phase. The secondconstruction algorithm is your choice.b$.$ Use an improvement algorithm before the beginning of clustering phase.c$.$ Use an improvement algorithm within each vehicles tour. Make sure that it isdifferent from part $2.$bd$.$ Your files will be in this form: Construction x $+$ improvement y $+$ improvementz$3.$ While keeping the time, consider every algorithm you have tried. For instance, in parta, the clustering time must be included in time calculation as well as other usedalgorithms for that particular file$/$algorithm combination$\mathrm{.}4.$ If you tried any combination, provide their codes and store their tour costs and algorithmtimes to a table. From that table, select the best possible algorithm combinationaccording to the tour costs for each part $($Given costs are same, select the one takes lesstime$).$Combination cost timeExample for part a: Cheapest Insertion $+2-$opt $10003$ secCheapest Insertion $+2-$exchange $9955$ secExample for part b: Cheapest Insertion $+2-$exchange$+2-$opt $10007$ secCheapest Insertion $+2-$opt$+2-$exchange $99010$ sec$5.$ For every solution, write a code that checks whether the vehicle capacity is violated tomake sure that you obtain a feasible solution$\mathrm{.}6.$ Bonus: After you obtain the best VRP solution for each part at part $4,$ code $2-$Exchange improvement between vehicle routes.c$.$ Find the VRP$-$Gurobi file from yulearn and run it for $10$ minutes. Apply the code on part$5$ above to the output as well. Besides, provide its mathematical formulation to a Wordor latex file. Note that Print screens are not allowed!The structure of the file must conform to the following style:$-$SetsSet symbol Definition$-$ParametersParameter symbol Definition$-$Decision variablesVariable symbol Definition$-$Mathematical Model$-$a group of equations$-$ Explanation of the mathematical modelExample: Objective function $($equation number$)$ explains thatConstraint $($eq number$)$ mentions that coordinates

demands

coordinates

$\backslash$table$[[,$Demand,,,,$],[0,0,$Node ID$,$x $-$coordinate,y$-$coordinate$],[1,18,0,39,19],[2,16,1,79,19],[3,22,2,41,79],[4,24,3,25,31],[5,3,4,63,93],[6,19,5,33,5],[7,6,6,69,17],[8,6,7,57,73],[9,6,8,53,75],[10,12,9,1,1],[11,18,10,79,73],[12,16,11,59,5],[13,72,12,1,37],[14,7,13,41,31],[15,16,14,23,73],[16,23,15,37,27],[17,4,16,85,93],[18,22,17,93,13],[19,23,18,85,45],[20,7,19,49,91],[21,11,20,55,43],[22,11,21,83,29],[23,1,22,93,49],[24,22,23,87,23],[25,16,24,31,23],[26,15,25,19,97],[27,75,26,41,9],[\backslash$table$[[28],[29]],5,27,83,61],[29$

$30,229,28,9,7],[\backslash$table$[[30],[31],[22]],910,29,13,13],[32,11,30,43,37],[33,9,31,13,61],[34,3,32,71,51],[35,7,33,45,93],[36,15,34,93,55],[37,10,35,5,97],[38,2,36,81,11],[,37,7,53],[,38,7,41]]$

coordinates

demands

coordinates

demands