It is a Stat Question

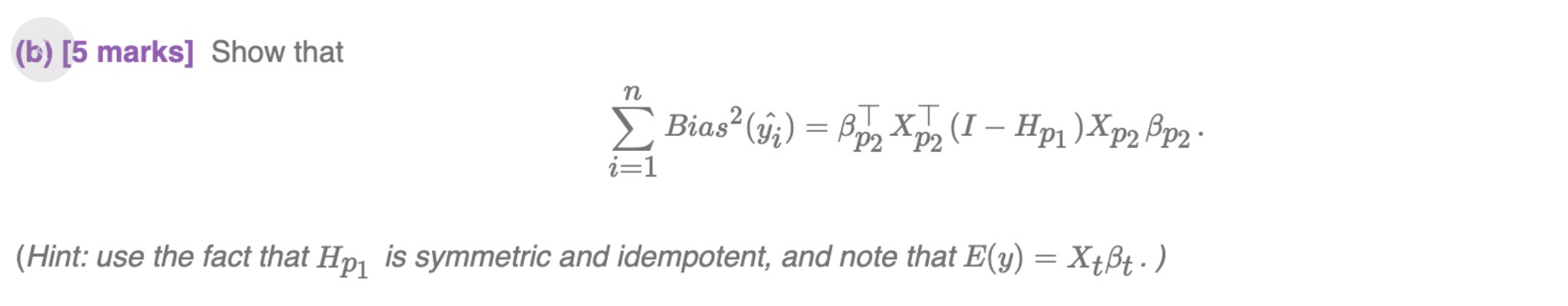
Question 1. [15 marks] In this question we consider derivation of Mallows' 0,, statistic for model selection discussed in lectures. Suppose the experimenter proposes a model 9 2 X171 p1 + 61 (P1 parameters), where Xp1 is n x p1 matrix and vector 5m contains p1 parameters. The "true\" model however contains additional p2 parameters described by vector 181,2. So the "true" model is given by 3/ = Xtt + 5 (P1 + p2 parameters), where Xtt = XPI pl + Xp2 p2 . In this model X112 is n X 122 matrix and 3172 contains p2 parameters. Assume that errors 6 are uncorrelated with mean zero and common variance 02. Consider fitting the proposed general linear model to data and write 321' for the fitted value at mi and MSE(g)i) for its mean squared error. Recall that if the error variance 02 is known, then an estimator of L1 MSELIM _ 2L1 me.) + Z?=1Bia32(r) 2 _ 02 2 0' 0' is n 5-202 121+ ( \"1'2 ), (1) where 62 is the estimator of the error variance and p1 is the number of parameters for the proposed model. You now have to provide a justification for (1). (1) [5 marks] Show that Bias?(yi) = Bp2 Xp2 (I - Hp1 ) Xp2 Pp2 . (Hint: use the fact that Hp, is symmetric and idempotent, and note that E(y) = XtBt. )