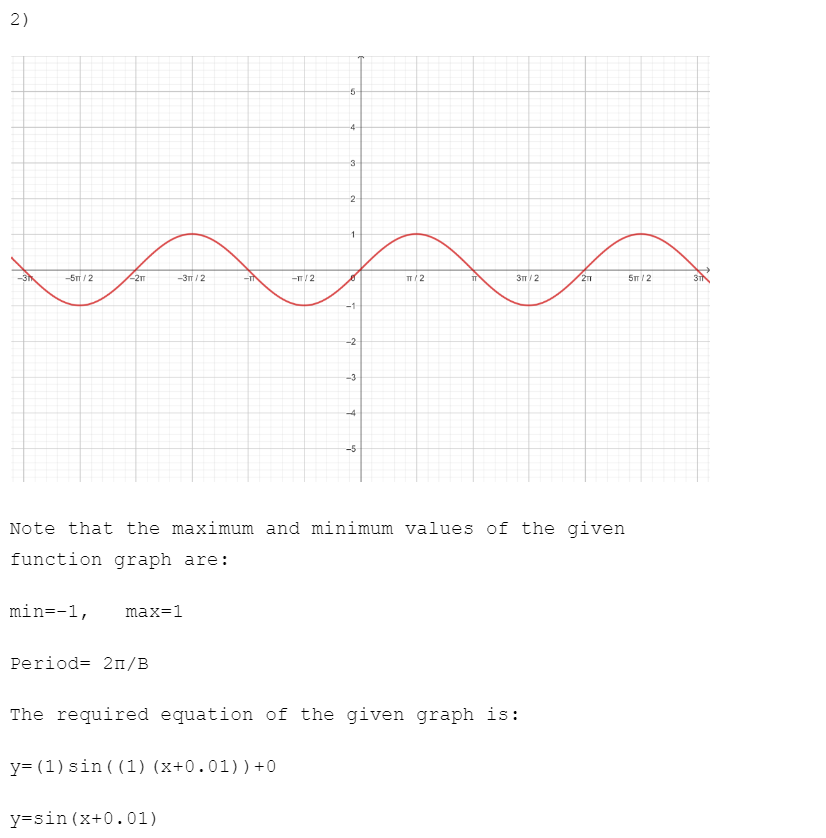
It is often the case that more than one sinusoidal function can be used to model the movement of a periodic function. Examine the example periodic function given below and determine an equation.

For this discussion,

1) Post an equation you got for the given graph.

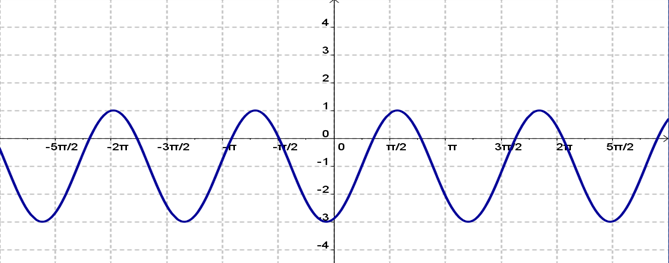
2) Create your own graph of a transformed trigonometric function and giveONE possible equation for it.

a) Post your graph and equation to the Discussions.

c) Make sure your equation is different from my example.

1) Recall that the formula for the sinusoid function is: v=hsiniEix+c3}+j Where A is the amplitude [half the distance between the maximum and minimum value), B determines the period, C determines the horizontal shifts, and D gives the vertical shifts [half the way between the maximum and minimum value}. Note that the maximum and minimum values of the given function graph are: min=3, max=l Find the value of amplitude [A]: Find the value of the vertical shifts (3]: D=l+[3}f2 n=1 Recall that the period for the sine or cosine function is: Period=2th Note that the period of the given function graph is: \f\f\f