It is one problem for all the questions, help please!!

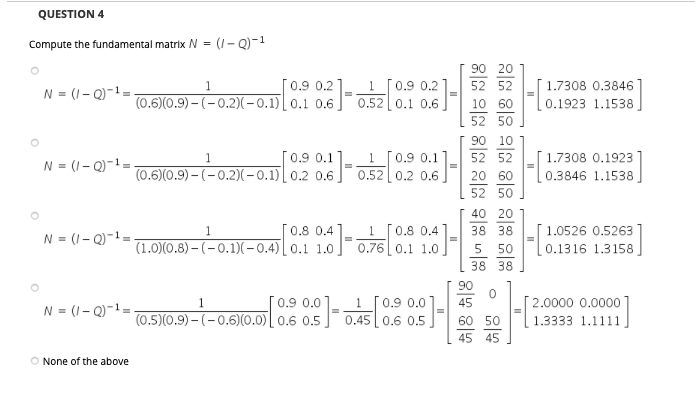
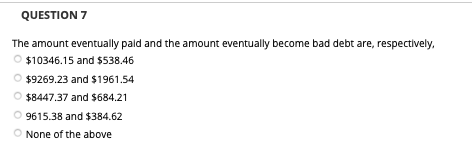
QUESTION 1 The same scenario is used for all questions. A psychiatrist clinic classifies its accounts receivable Into the following four states State 1. Pald State 2. Bad debt State 3.0-30 days State 4. 31-90 days Using a Markov process model with the preceding states, we define the transition probabilities as follows: Py = probability of a dollar in state / In one week moving to state / In the next week. Based on the historical transition from week to week of accounts receivable, the following matrix of transition probabilities has been developed for the clinic 1.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 P= 0.5 0.0 0.4 0.1 0.6 0.1 0.2 0.1 Identify the absorbing and non-absorbing states: A. State 1. Pald category - ABSORBING STATE State 2. Bad debt category - NON-ABSORBING STATE State 3.0-30-day category - ABSORBING STATE State 4. 31-90-day category - NON-ABSORBING STATE B. State 1. Pald category - NON-ABSORBING STATE State 2. Bad debt category - ABSORBING STATE State 3.0-30-day category - NON-ABSORBING STATE State 4. 31-90-day category - ABSORBING STATE C. State 1. Pald category - ABSORBING STATE State 2. Bad debt category - ABSORBING STATE State 3.0-30-day category - NON-ABSORBING STATE State 4. 31-90-day category - NON-ABSORBING STATE D. State 1. Pald category - NON-ABSORBING STATE State 2. Bad debt category - NON-ABSORBING STATE State 3.0-30-day category - ABSORBING STATE State 4.31-90-day category - ABSORBING STATE QUESTION 3 The matrix IQ can be calculated as: 1.0 0.0 0.4 0.2 0.0 1.0 0.1 0.1 1 - Q = 1.0 0.0 0.0 0.4 0.0 1.0 0.1 0.1 1.0 0.0 0.0 0.0 1.0 1.0 0.0 0.4 0.1 1 - Q = 0.0 1.0 0.2 0.1 1 - Q = [ 0:0 1:0] - [ 0.1 0.2 ]- :2]-[- = [ :0 1:0) - [0:2 0:1 ]-[-02 0.6 -0.2 -0.1 0.9 1.0 -0.4 -0.1 0.8 0.5 0.01 -0.6 0.9 0.6 -0.1 -0.2 0.9 None of the above QUESTION 4 Compute the fundamental matrix N = (1-0)-1 1 N = (1-0)-1= (0.6)(0.9)-(-0.2)(-0.1) 0.1 0.6 0:] 1.7308 0.3846 0.1923 1.1538 N = (1-0)-1- 1 0.9 0.11 (0.6)(0.9)-(-0.2)(-0.1) 0.2 0.6 1 [0.9 0.1 0.52 0.2 0.6 1.7308 0.1923 0.3846 1.1538 90 20 52 52 10 60 52 50 90 10 52 52 20 60 52 50 40 20 38 38 5 50 38 38 90 0 45 60 50 45 45 0.8 0.4 N = (1-0)-1- (1.0)(0.8)-(-0.1)(-0.4)(0.1 1.0 1 [0.8 0.4 0.76 0.1 1.0 0.6) 1.0526 0.5263 0.1316 1.3158 N = (1-0)-1- 1 [0.9 0.0 0.45 0.6 0.5 (0.5)(0.9)-(-0.6)(0.0 | 0.6 0.5 [2.0000 0.0000 1.3333 1.1111 None of the above QUESTION 5 Find the matrix NR of probabilities that the accounts receivable in states 3 and 4 will eventually reach one of the absorbing states. NR = [ 1.7308 0.3846 0.5 0.0 1.0962 0.0385 0.7885 0.1154 1.0526 0.5263 T 0.5 0.0 0.8421 0.0526 NR = 0.1316 1.3158 0.6 0.1 0.8553 0.1316 1.7308 0.1923 T 0.5 0.0 0.9808 0.0192 NR = 0.3846 1.1538 0.6 0.1 0.8846 0.1154 1.7308 0.1923 0.5 0.1 1.0192 0.2115 NR = 0.3846 1.1538 0.4 0.1 0.5580 0.1346 = [ 1 6 0 11-(0.89 0:0) -[ 0.88 10:4 0:1 ][ 0.5 None of the above QUESTION 6 The clinic currently has $8000 accounts receivable in the 0-30 days state and $2000 in the 31-90 days state. Find how much of the current accounts receivable will eventually be paid, and how much will become bad debt. 0.9808 0.0192 BNR = [8000 2000 = [ 9615.38 384.62] BNR = [ 8000 2000 BNR = [ 8000 2000 0.8421 0.0526 = [ 8447.37 684.21] 0.8553 0.1316 1.0192 0.2115 = [ 9269.23 1961.54) 0.5580 0.1346) 1.0962 0.0385 10346.15 538.46] BNR = [ 8000 2000 None of the above QUESTION 7 The amount eventually paid and the amount eventually become bad debt are, respectively, $10346.15 and $538.46 $9269.23 and $1961.54 $8447.37 and $684.21 9615.38 and $384.62 None of the above