It is part C answer

Questions

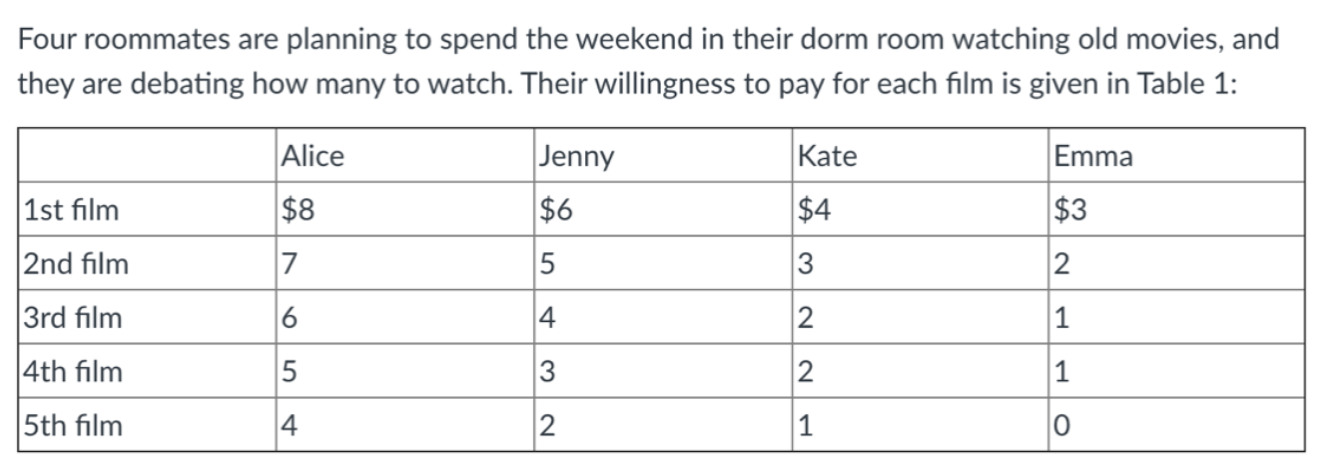
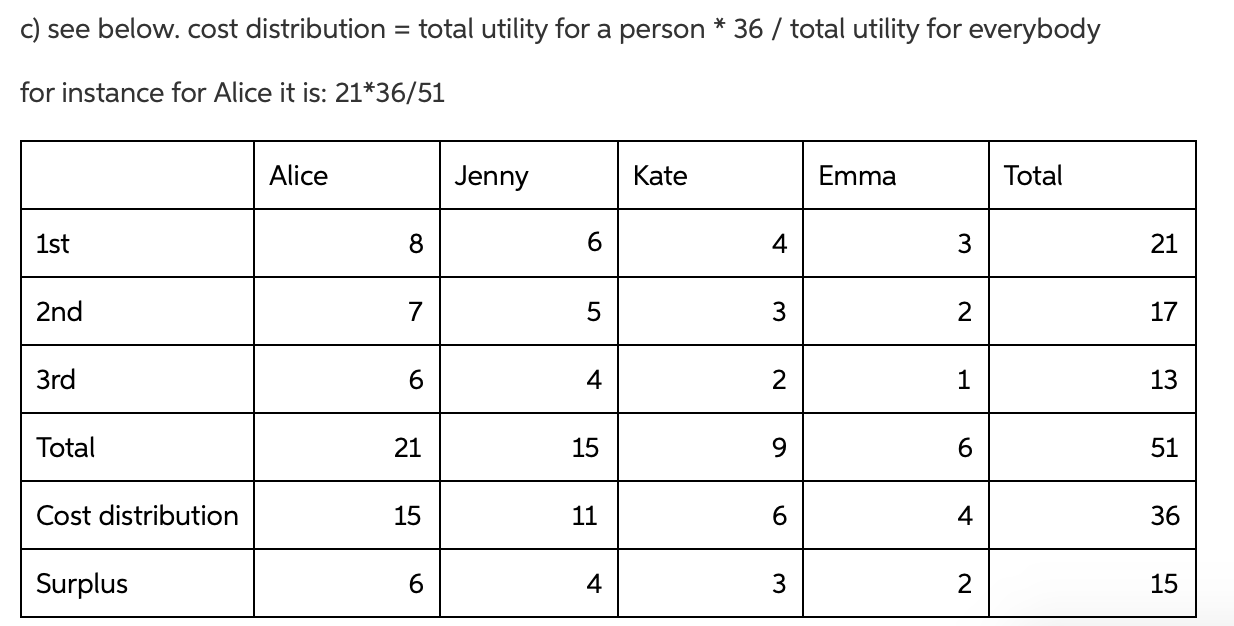
Four roommates are planning to spend the weekend in their dorm room watching old movies, and they are debating how many to watch. Their willingness to pay for each film is given in Table 1: Alice Kate Emma Jenny $6 1st film $8 $4 $3 2nd film 7 5 3 2 3rd film 6 4 2 1 |4th film 5 3 2 1 5th film 4 2 1 c) Suppose the 4 roommates choose the number of movies to rent in part a), and decide that the cost should be divided up by the roommates based on the benefits they receive (that is, person i pays share X; of the cost of movie m, where X;M= is value of movie m/total value of movie m). Does everyone benefit? (2 points) c) see below. cost distribution = total utility for a person * 36 / total utility for everybody for instance for Alice it is: 21*36/51 Alice Jenny Kate Emma Total 1st 8 6 4 3 21 2nd 7 5 3 2 17 3rd 6 4 2 1 13 Total 21 15 9 6 51 Cost distribution 15 11 6 4 36 Surplus 4 3 2 15 In reality, each roommate's willingness to pay is only known to herself, and the decision on renting movies can only be made based on their stated willingness to pay, which must be non-negative integer but might not be their true willingness to pay. Consider the case where the cost is divided up by the roommates based on the benefits they receive as in part c). Given this condition, answer the following questions. d) Suppose the roommates are considering whether to rent the 3rd movie. Suppose the roommates rent a movie when the total surplus from that movie is zero. Consider the strategy of Alice. Suppose when Alice expects the sum of the stated willingness to pay by Jenny, Kate and Emma is $a, she can just change the decision whether to rent the 3rd movie by stating her true willingness to pay for the 3rd movie. How large is a? In this case, what is the surplus to Alice from the 3rd movie if she states her true willingness to pay for the 3rd movie? What is the surplus to Alice from the 3rd movie if she under-states her true willingness to pay by $1? What is the surplus to Alice from the 3rd movie if she over-states her true willingness to pay by $1? (4 points) e) (i) When Alice expects the sum of the stated willingness to pay by Jenny, Kate and Emma is lower than $a, should Alice understate, truthfully state, or overstate her willingness to pay for the 3rd movie? (ii) When Alice expects the sum of willingness to pay by Jenny, Anna and Emma is higher than $a, should Alice understate, truthfully state, or overstate her willingness to pay for the 3rd movie? (2 points) f) According to d) and e), when the cost is divided up by the roommates based on the stated benefits they receive, is it a dominant strategy for Alice to understate her willingness to pay? Why? Does this apply to other roommates? How does the number of movies rented in a Nash Equilibrium compared to the efficient level? (2 points) Four roommates are planning to spend the weekend in their dorm room watching old movies, and they are debating how many to watch. Their willingness to pay for each film is given in Table 1: Alice Kate Emma Jenny $6 1st film $8 $4 $3 2nd film 7 5 3 2 3rd film 6 4 2 1 |4th film 5 3 2 1 5th film 4 2 1 c) Suppose the 4 roommates choose the number of movies to rent in part a), and decide that the cost should be divided up by the roommates based on the benefits they receive (that is, person i pays share X; of the cost of movie m, where X;M= is value of movie m/total value of movie m). Does everyone benefit? (2 points) c) see below. cost distribution = total utility for a person * 36 / total utility for everybody for instance for Alice it is: 21*36/51 Alice Jenny Kate Emma Total 1st 8 6 4 3 21 2nd 7 5 3 2 17 3rd 6 4 2 1 13 Total 21 15 9 6 51 Cost distribution 15 11 6 4 36 Surplus 4 3 2 15 In reality, each roommate's willingness to pay is only known to herself, and the decision on renting movies can only be made based on their stated willingness to pay, which must be non-negative integer but might not be their true willingness to pay. Consider the case where the cost is divided up by the roommates based on the benefits they receive as in part c). Given this condition, answer the following questions. d) Suppose the roommates are considering whether to rent the 3rd movie. Suppose the roommates rent a movie when the total surplus from that movie is zero. Consider the strategy of Alice. Suppose when Alice expects the sum of the stated willingness to pay by Jenny, Kate and Emma is $a, she can just change the decision whether to rent the 3rd movie by stating her true willingness to pay for the 3rd movie. How large is a? In this case, what is the surplus to Alice from the 3rd movie if she states her true willingness to pay for the 3rd movie? What is the surplus to Alice from the 3rd movie if she under-states her true willingness to pay by $1? What is the surplus to Alice from the 3rd movie if she over-states her true willingness to pay by $1? (4 points) e) (i) When Alice expects the sum of the stated willingness to pay by Jenny, Kate and Emma is lower than $a, should Alice understate, truthfully state, or overstate her willingness to pay for the 3rd movie? (ii) When Alice expects the sum of willingness to pay by Jenny, Anna and Emma is higher than $a, should Alice understate, truthfully state, or overstate her willingness to pay for the 3rd movie? (2 points) f) According to d) and e), when the cost is divided up by the roommates based on the stated benefits they receive, is it a dominant strategy for Alice to understate her willingness to pay? Why? Does this apply to other roommates? How does the number of movies rented in a Nash Equilibrium compared to the efficient level? (2 points)