It is requested to represent the following problems as linear programming models (PL). Should be Define decision variables, objective function and constraints. The restrictions are due number.

It is a linear programation problem, what do you need?

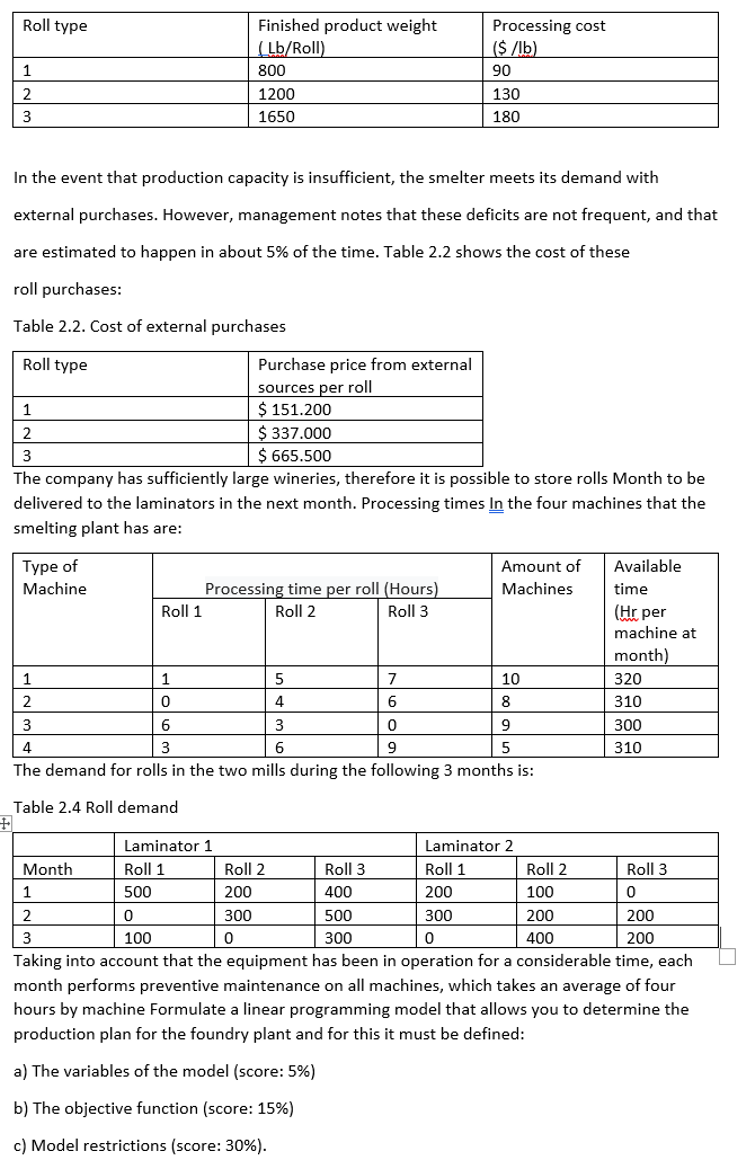
Roll type Finished product weight (Lb/Roll) 800 1200 1650 Processing cost ($ /lb) 90 130 180 In the event that production capacity is insufficient, the smelter meets its demand with external purchases. However, management notes that these deficits are not frequent, and that are estimated to happen in about 5% of the time. Table 2.2 shows the cost of these roll purchases: Table 2.2. Cost of external purchases Roll type Purchase price from external sources per roll 1 $ 151.200 $ 337.000 $ 665.500 The company has sufficiently large wineries, therefore it is possible to store rolls Month to be delivered to the laminators in the next month. Processing times in the four machines that the smelting plant has are: Type of Machine Amount of Machines Processing time per roll (Hours) Roll 1 Roll 2 Roll 3 Available time (Hr per machine at month) 320 310 300 310 | 7 10 6 8 6 3 0 9 3 6 9 5 The demand for rolls in the two mills during the following 3 months is: Table 2.4 Roll demand Laminator 1 Laminator 2 Month Roll 1 Roll 2 Roll 3 Roll 1 Roll 2 Roll 3 500 200400 200 100 | 2 o 300 500 300 200 200 3 100 300 0 400 200 Taking into account that the equipment has been in operation for a considerable time, each month performs preventive maintenance on all machines, which takes an average of four hours by machine Formulate a linear programming model that allows you to determine the production plan for the foundry plant and for this it must be defined: JO a) The variables of the model (score: 5%) b) The objective function (score: 15%) c) Model restrictions (score: 30%). Roll type Finished product weight (Lb/Roll) 800 1200 1650 Processing cost ($ /lb) 90 130 180 In the event that production capacity is insufficient, the smelter meets its demand with external purchases. However, management notes that these deficits are not frequent, and that are estimated to happen in about 5% of the time. Table 2.2 shows the cost of these roll purchases: Table 2.2. Cost of external purchases Roll type Purchase price from external sources per roll 1 $ 151.200 $ 337.000 $ 665.500 The company has sufficiently large wineries, therefore it is possible to store rolls Month to be delivered to the laminators in the next month. Processing times in the four machines that the smelting plant has are: Type of Machine Amount of Machines Processing time per roll (Hours) Roll 1 Roll 2 Roll 3 Available time (Hr per machine at month) 320 310 300 310 | 7 10 6 8 6 3 0 9 3 6 9 5 The demand for rolls in the two mills during the following 3 months is: Table 2.4 Roll demand Laminator 1 Laminator 2 Month Roll 1 Roll 2 Roll 3 Roll 1 Roll 2 Roll 3 500 200400 200 100 | 2 o 300 500 300 200 200 3 100 300 0 400 200 Taking into account that the equipment has been in operation for a considerable time, each month performs preventive maintenance on all machines, which takes an average of four hours by machine Formulate a linear programming model that allows you to determine the production plan for the foundry plant and for this it must be defined: JO a) The variables of the model (score: 5%) b) The objective function (score: 15%) c) Model restrictions (score: 30%)