It's an assignment about dynamic programming.

Description An adorable, but lazy, quokka is descending through the branches of a tree, eating leaves on its way home to sleep. The tree is represented by a matrix w wide and h high. Each position is an integer, representing how tasty the leaves are. These integers can be negative, because some of the leaves have bugs on. Start point: The quokka always starts in the top right corner of the tree (i.e. position (w, h)). This corner of the tree will always have a value of 0. End point: The quokka wants to go home to its nest at the bottom left corner of the tree (i.e. position (1, 1)). Jumping down: The quokka can jump directly down to a new row. It can skip zero or more rows when it does this, but it will always eats the leaf it lands upon. Hopping left: The quokka can hop to the left, one step at a time, eating every leaf it finds, even if it is not tasty (its hungry!) Because it is a lazy quokka and has tiny legs, it quickly gets tired each consecutive step to the left incurs a score penalty: The first step left costs 1 point The second consecutive left costs 2 points The third consecutive left costs 3 points etc. Happily, it enjoys jumping so much that whenever it moves down to a new branch it forgets how tired its little feet were getting. Therefore the next time it decides to move left, the penalty cost will be back down to just 1 point again. Other directions The quokka never moves right or upwards, because it is sleepy and wants to get home quickly. Objective Use dynamic programming to calculate the maximum happiness that the quokka can achieve at the end of its journey from the top right to the bottom left. The quokkas happiness is defined by the sum of the leaves it ate, minus the penalties accumulated from hopping left along the branches.

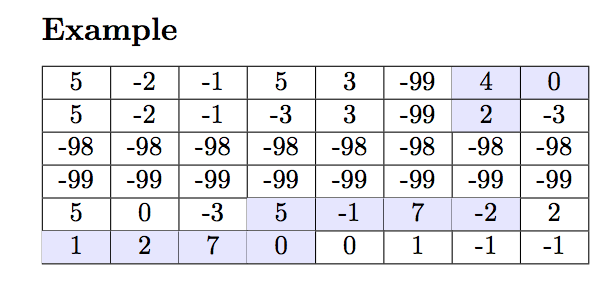
This example tree has dimensions h = 6, w = 8. The leaves eaten by the quokka on an optimal path through the tree are shaded. Note that it dropped directly from the 2 to the -2, skipping the -98 and -99, because it fell past them, but it ate the -2 leaf because it landed on it. It also ate the -1 leaf on the second row, because it cannot skip leaves when moving left. The score for this path can be calculated like this:

Tasks Task 1: [10 marks] Define the subproblems needed by your algorithm (i.e. what does the function OP T(...) represent, and what are its parameters.) Task 2: [20 marks] Define the recurrence(s) and base case(s) (i.e. give the mathematical functions OP T(...) =?) Task 3: [30 marks] Justify the correctness of your algorithm. In particular, take care to prove that the recurrence is correct the base case(s) are correct and sufficient Task 4: [20 marks] State and explain the complexity of your algorithm (in big-Oh notation). Consider both: 1. Time complexity 2. Space complexity Make sure you justify the answers you give, dont merely state the values.

Example 5-2153-9940 3399 2-3 5-21 -99 -99-9999-9999-9999 50 -35-1 7-22 12 70 011