Its easy discreet math. Translate from norwegian

Exercise 6:

A Boolean function in three variables, F (x, y, z), has output as in the table below. a) Make Sum of product development to F (x, y, z). b) Use the Karnaugh maps or Quine-Maclaskey algorithm to simplify the expression for F (x, y, z) (what you found in b).

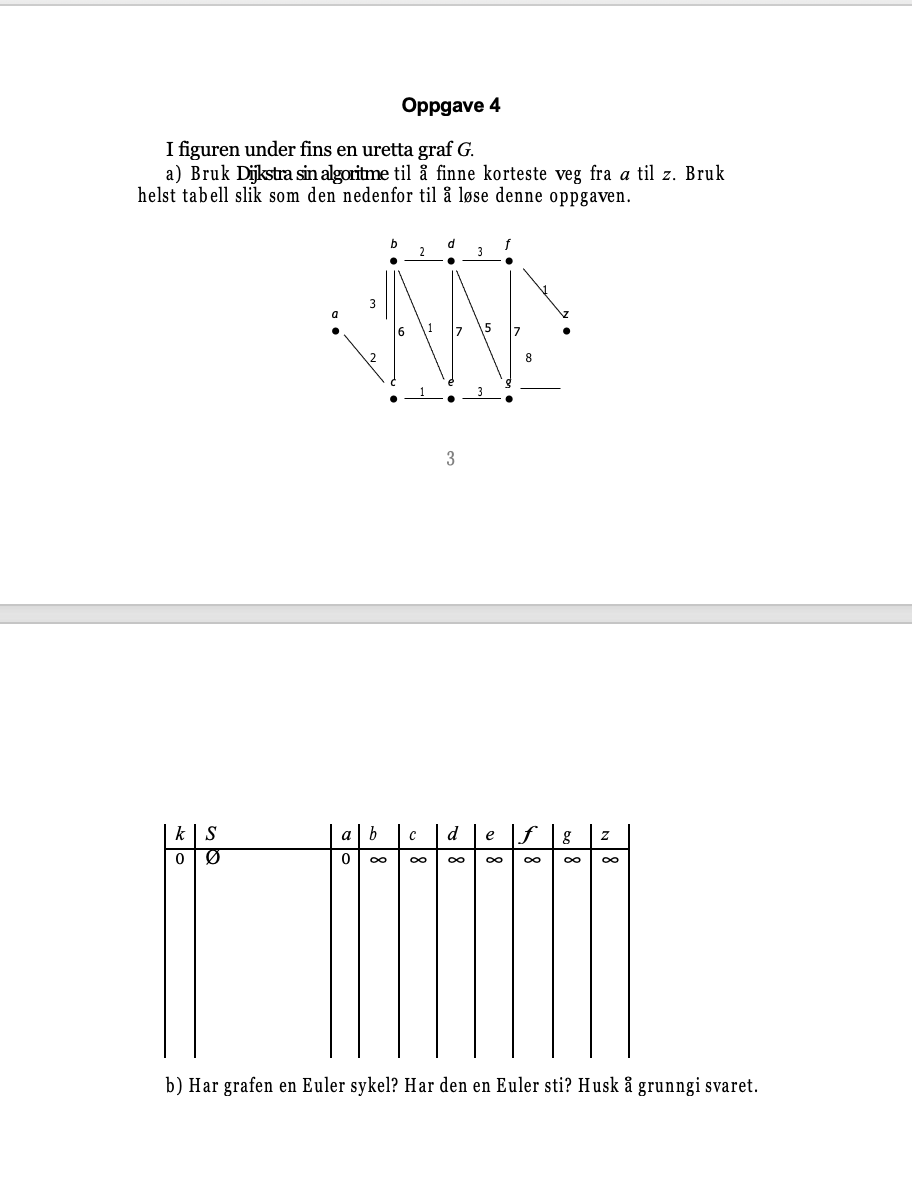
Exercise 4

In the figure below there is an incorrect graph G. a) Use Dijkstra's algorithm to find the shortest path from a to z. Preferably use a table such as the one below to solve this problem.

b) Does the graph have an Euler cycle? Does it have an Euler trail?

Remember to base the answer.

Oppgave 6 En Boolsk funksjon i tre variabler, F (x, y, z), har output som i tabellen under. a) Lag Sum av produktutviklinga til F (x, y, z). b) Bruk Karnaugh maps eller Quine-Maclaskey algoritmen til forenkle uttrykket for F(x, y, z) (det du fant i b). 5 x yZF (x, y, z) 1 1 1 1 1 0 0 1 1 1 1 0 0 0 0 1 1 1 0 1 0 0 0 1 0 1 00 0 1 Oppgave 4 I figuren under fins en uretta graf G. a) Bruk Dijkstra sin algoritme til finne korteste veg fra a til z. Bruk helst tabell slik som den nedenfor til lse denne oppgaven. b 2 d 3 . 3 a 6 7 8 3 ks a b d e f 8 Z 0 0 oo oo 18 oo b) Har grafen en Euler sykel? Har den en Euler sti? Husk grunngi svaret