It's supposed to be a minimization problem. So the LINDO needs to be changed to min

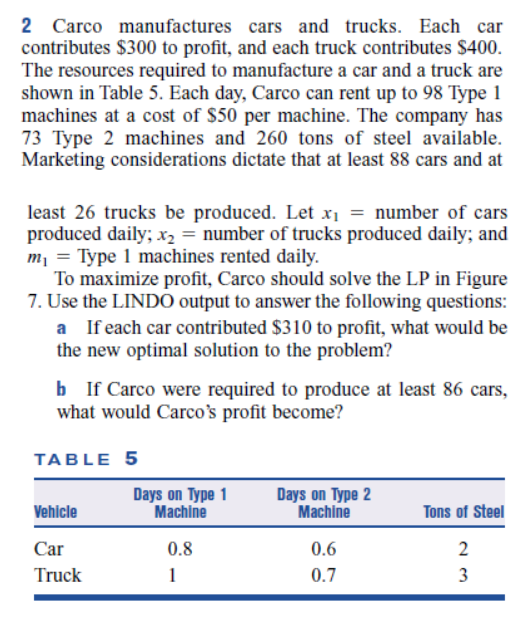
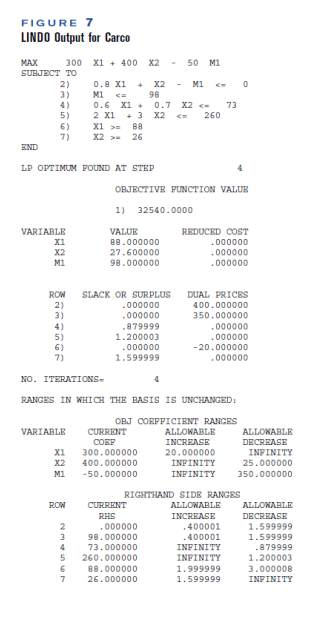
2 Carco manufactures cars and trucks. Each car contributes $300 to profit, and each truck contributes $400. The resources required to manufacture a car and a truck are shown in Table 5. Each day, Carco can rent up to 98 Type 1 machines at a cost of $50 per machine. The company has 73 Type 2 machines and 260 tons of steel available. Marketing considerations dictate that at least 88 cars and at least 26 trucks be produced. Let x1= number of cars produced daily; x2= number of trucks produced daily; and m1= Type 1 machines rented daily. To maximize profit, Carco should solve the LP in Figure 7. Use the LINDO output to answer the following questions: a If each car contributed $310 to profit, what would be the new optimal solution to the problem? b If Carco were required to produce at least 86 cars, what would Carco's profit become? TABLE 5 FIGURE 7 LINDO Output for Carco LP OPTIMTM POUND AT STED OBJECTIVB BUNCTION VALU 1) 32540.0000 NO. ITERNTIONS- 4 RANGES IN WHICH THE BASIS IS UNCHANGED