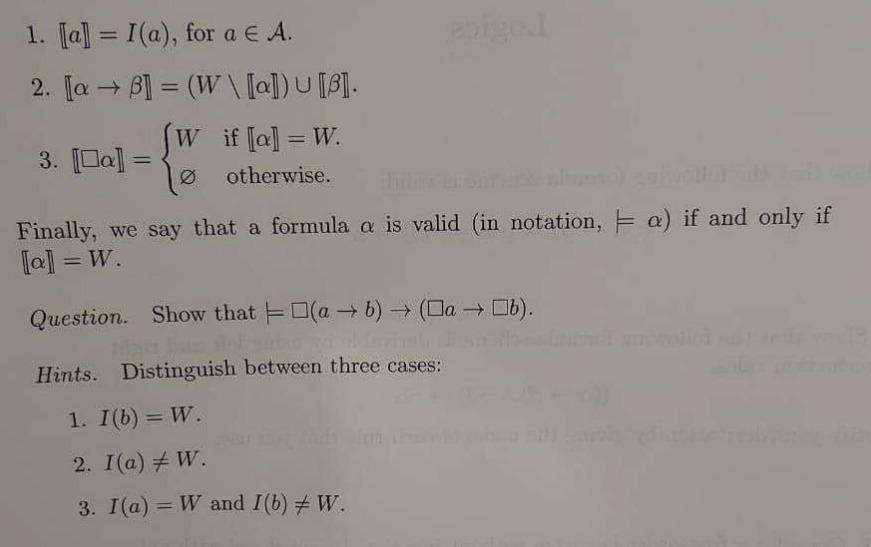
IV. Context. We consider a logical calculus which is known as the implicative fragment of modal logic. The formulas of this calculus are built upon a countable set A of atomic propositions, according to the following inductive definition: 1. Every atomic proposition is a formula. 2. If and are formulas so is (). 3. If is formula so is . Given a set W, the elements of which are called possible worlds, the formulas will be interpreted as sets of possible worlds (i.e., subsets of W ). Accordingly, one defines a model to be a function from A into 2W. Then, given such a model, say I, the interpretation of the formulas is inductively defined as follows: 1. [[a]]=I(a), for aA. 2. [[]]=(W\[[]])[[]]. 3. [[]]={Wif[[]]=W.otherwise. Finally, we say that a formula is valid (in notation, ) if and only if [[]]=W Question. Show that (ab)(ab). Hints. Distinguish between three cases: 1. I(b)=W. 2. I(a)=W. 3. I(a)=W and I(b)=W