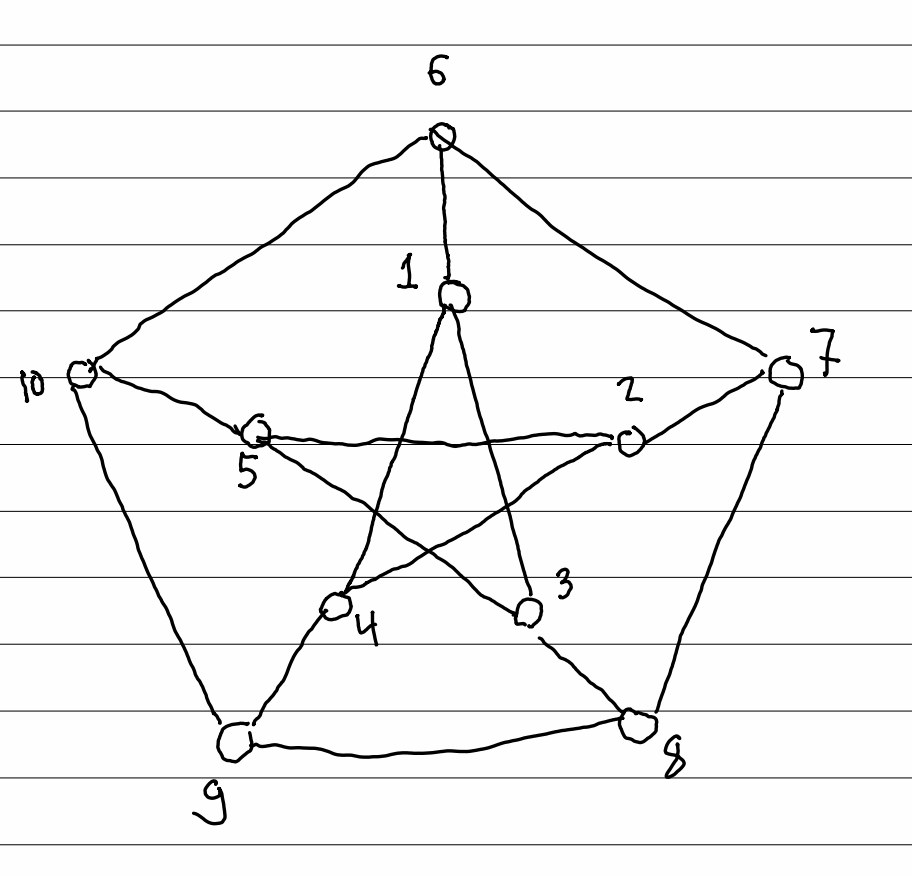
J S 9Let T : V > V be the adjacency operator of the Petersen graph as illustrated in the enclosed file. Here V is the vector space of all formal real linear combinations of the vertices v1, , 010 of the Petersen graph. 1. Show that the subspace spanned by u = 01 + 02 + 03 + 04 + 05 and w = ()5 + 07 + 03 + Ug + 010 is stable under T, by calculating T(u) and T(w) explicitly. 2. Use part 1 to calculate (by hand) an eigenvector for T satisfying T(v) = 30, and an eigenvector satisfying T(U) = v. 3. (Extra credit). Use Pari to compute the spectrum of the adjacency operator T of the Petersen graph. What do you observe