java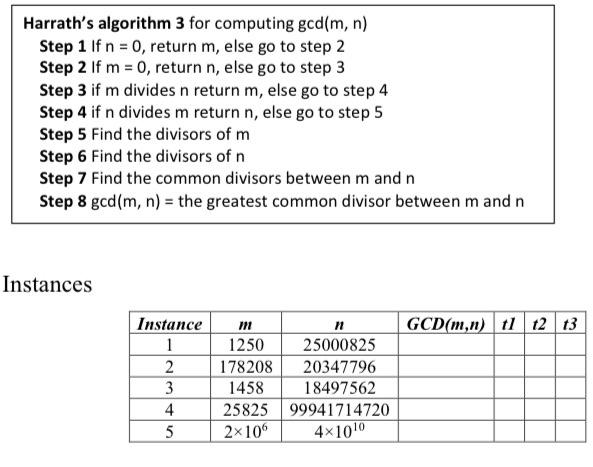

1. Code the three algorithms covered in Chapter 1 to solve the Greatest Common Divisor (use long as number types). 2. Provide the running times of the different algorithms using the given instances. 3. Use MS Excel to draw a bar chart diagram illustrating the running times of each problem instance using each algorithm (Similar to the given diagram). Running times of different algorithms 20 0 rt3 rt 2 Instances 11 12 13 Algorithms ALGORITHM1 Euclid(m, n) Input: Two non-negative, not-both-zero integers m and n Output: Greatest Common Divisor of mand n while n+ 0 do rem mod n men ner return m ALGORITHM 2 CICA(m, n) Input: Two non-negative, not-both-zero integers m and n Output: Greatest Common Divisor of mand n tt min(m, n) stop false while stop = false do If m mod t = 0 AND n mod t = 0 stop = true; Elset tt-1 returnt Harrath's algorithm 3 for computing gcd(m, n) Step 1 If n = 0, return m, else go to step 2 Step 2 If m = 0, return n, else go to step 3 Step 3 if m divides n return m, else go to step 4 Step 4 if n divides m return n, else go to step 5 Step 5 Find the divisors of m Step 6 Find the divisors of n Step 7 Find the common divisors between m and n Step 8 gcd(m, n) = the greatest common divisor between m and n Instances GCD(m,n) 11 12 13 Instance 1 2 3 4 5 n 1250 25000825 178208 20347796 1458 18497562 25825 99941714720 2x106 4x1010