JAVA:

Algorithm developed by Carl Friedrich Gauss in 1800 consists of the following steps:

1. Let y by the year (such as 1800 or 2001).
2. Divide y by 19 and call the remainder a. Ignore the quotient.
3. Divide y by 100 to get a quotient b and a remainder c.
4. Divide b by 4 to get a quotient d and a remainder e.
5. Divide 8 * b + 13 by 25 to get a quotient g. Ignore the remainder.
6. Divide 19 * a + b - d - g + 15 by 30 to get a remainder h. Ignore the quotient.
7. Divide c by 4 to get a quotient j and a remainder k.
8. Divide a + 11 h by 319 to get a quotient *m. Ignore the remainder.
9. Divide 2 * e + 2 * j - k - h + m + 32 by 7 to get a remainder r. Ignore the quotient.
10. Divide h - m + r + 90 by 25 to get a quotient n. Ignore the remainder.
11. Divide h - m + r + n + 19 by 32 to get a remainder p. Ignore the quotient.

I need to implement an algorithm inside of the Constructor for the GaussianEaster object. All the rest of the variables mentioned in the algorithm should be local variables, not instance variables.

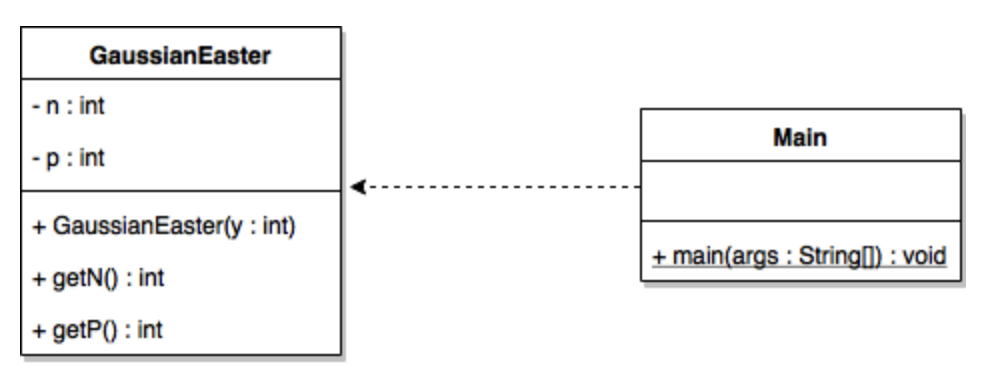
NOTE: UML are backwards from Java code (e.g. y : int is int y in Java).

The Gaussian.java class computes the month and day of Easter given the year. The only instance variables allowed are n (the month) and p (the day).

As for the Main.java class is for testing the Gaussian object

GaussianEaster n:int p: int +GaussianEaster(y: int) +getNO : int .::.tycs@R'O : ilt Main +main(args : Stringl) : void