JAVA CODE ! The book is Data Abstraction and Problem Solving with Java: Walls and Mirrors, 3rd Edition

I NEED HELP WITH QUESTION 4

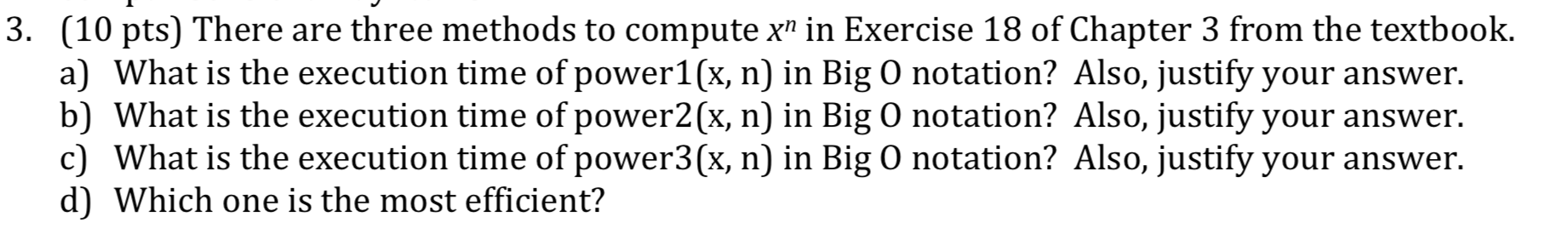
HERES THE CODE FOR QUESTION 4

public static void power1(long x,long n)

{

long ans = 1,mulCount = 0;

for(int i = 1;i

{

ans = ans*x;

mulCount += 1;

}

System.out.println("Result from power 1 :" + ans);

System.out.println("Number of multiplications from power 1 :" + mulCount + " ");

}

public static long power2(long x,long n)

{

if(n != 0)

{

rec2Count += 1;

mul2Count += 1;

return (x * power2(x,n-1));

}

else

return 1;

}

public static long power3( long x, long n)

{

if ( n == 0 )

{

return 1;

}

long powerOfHalfN = power3( x, n/2 );

rec3Count += 1;

if ( n % 2 == 1 )

{

// Odd n

mul3Count += 2;

return x * powerOfHalfN * powerOfHalfN;

}

else

{

// Even n

mul3Count += 1;

return powerOfHalfN * powerOfHalfN;

}

}

}

3. (10 pts) There are three methods to compute xn in Exercise 18 of Chapter 3 from the textbook. a) What is the execution time of power1(x, n) in Big O notation? Also, justify your answer. b) What is the execution time of power2(x, n) in Big O notation? Also, justify your answer. c) What is the execution time of power3(x, n) in Big O notation? Also, justify your answer. d) Which one is the most efficient? 4. (10 pts) An array of doubles can be used to represent a polynomial of one variable. The index of an item in the array represents the exponent, and the value of the array element is the coefficient of the term. For example, if the polynomial p(x) = 10x15 - 3.2x8 + x + 7.5 and is represented by an array p[], then p[15] = 10.0, p[8] = -3.2, p[1] = 1.0, p[0] = 7.5, and the other items in the array are zeroes. The degree of a polynomial is the exponent of its highest term. For example, the degree of p(x) above is 15. The method evaluate(x) can be implemented in several different ways. What is the execution time of each implementation described below in Big O notation? Also, justify each answer. a) Implementation 1: value = 0; for (int i = 0; i = 0; i--) // d is the degree of the polynomial value = value * x + p[i]; return value; d) Which one is the most efficient? 3. (10 pts) There are three methods to compute xn in Exercise 18 of Chapter 3 from the textbook. a) What is the execution time of power1(x, n) in Big O notation? Also, justify your answer. b) What is the execution time of power2(x, n) in Big O notation? Also, justify your answer. c) What is the execution time of power3(x, n) in Big O notation? Also, justify your answer. d) Which one is the most efficient? 4. (10 pts) An array of doubles can be used to represent a polynomial of one variable. The index of an item in the array represents the exponent, and the value of the array element is the coefficient of the term. For example, if the polynomial p(x) = 10x15 - 3.2x8 + x + 7.5 and is represented by an array p[], then p[15] = 10.0, p[8] = -3.2, p[1] = 1.0, p[0] = 7.5, and the other items in the array are zeroes. The degree of a polynomial is the exponent of its highest term. For example, the degree of p(x) above is 15. The method evaluate(x) can be implemented in several different ways. What is the execution time of each implementation described below in Big O notation? Also, justify each answer. a) Implementation 1: value = 0; for (int i = 0; i = 0; i--) // d is the degree of the polynomial value = value * x + p[i]; return value; d) Which one is the most efficient