JAVA!! follow TEST, sorry for many pictures

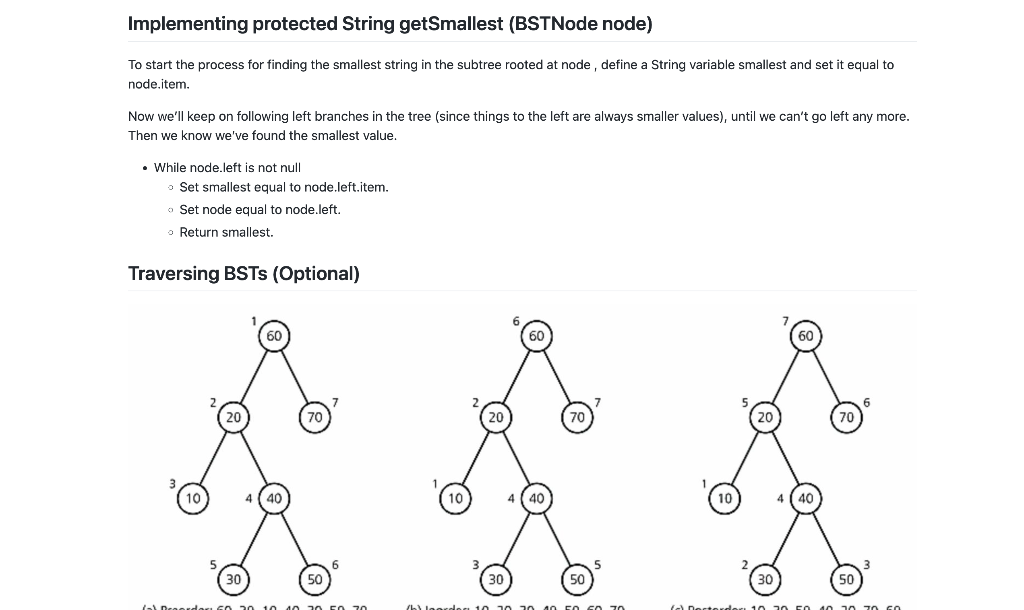
In this assignment, you will be creating a binary search tree (BST). The tree will be storing words ( Strings ), which you will insert, as well as delete, recursively. You will also be implementing tree traversals, which are different orders in which you recursively visit the items in a tree. Testing - Testing can be done through Maven with the command, mvn test - To run more specific tests, run the command mvn -Dtest=BinarySearchTree\#TESTCASEHERE test where TESTCASEHERE is the test case you want to run. These test cases can be found in src/test/java/BinarySearchTreeTest For example, mvn -Dtest=BinarySearchTree\#test_put test tests your put method. The results can be found in the command line or in target/surefire-reports/BinarySearchTreeTest.txt after execution. Part of grading will be these test cases. Alternatively, To test your BST, the main() in TestBST.java creates an instance of your BST and tests it. It makes use of the printTreeStructure() method that we've provided on BinarySearchTree. This prints out the internal structure of the tree so you can verify your operations are behaving correctly. Implementing a BST You will be creating a BST using a BST class called BinarySearchTree. It implements the interface BSTInterface . BSTNodes will be used to store an item which in this assignment are Strings. It will also contain references to its left and right subtrees (which as also BSTNodes ). The BSTNode constructor will initialize the item to a value and the left and right nodes to null . The BinarySearchTree class itself only has one field, the root of the BST. The constructor for the BinarySearchTree only has to set the You will be implementing the following methods for your BST: - public boolean isEmpty () Returns true if BST is empty, false otherwise - public void makeEmpty () Clears BST so that it is empty - public MyQueue inOrder () - Returns a queue with the elements in-order - public MyQueue preOrder () - Returns a queue with the elements in pre-order - public MyQueve postOrder () - Returns a queue with the elements in post-order - public boolean contains (String s) Returns true if the BST contains the string, otherwise returns false - public void put (String s) - If the string is already in the BST, then put will do nothing. If the string is not in the BST, then put will add the string to the BST. - public void delete (String s) - Removes the specified string from the BST, if the string cannot be found, then delete does nothing Implementing public void put (String s) Implementing put ( String s ) will require creating a recursive helper method to assist with searching through the BST to find the appropriate place to put the new node. In your put ( String s) method, you will need to call recursivelnsert() with the root of your BST as one argument and the String to insert as the other. Set root equal to the node returned from recursivelnsert() . The way to think about this is that you're setting the root equal to the new tree that results from doing the recursive insert. Implementing protected BSTNode recursivelnsert (BSTNode node, String s) - You will have two cases to consider: 1) if node is null or 2) when node is not null. - When node is null, this means that you've come to an empty subtree. This is where you will create the new node. Return a new Implementing protected BSTNode recursivelnsert (BSTNode node, String s) - You will have two cases to consider: 1) if node is null or 2) when node is not null. - When node is null, this means that you've come to an empty subtree. This is where you will create the new node. Return a new BSTNode containing the String. - If node is not null, then you need to compare the String argument to the item in the node. - If the String s is alphabetically before node.item, then we want to set the left subtree of node ( node.left ) equal to recursively inserting s into the left subtree. - Similarly, if the String s is alphabetically after node.item, then we want to set the right subtree of node ( node.right ) equal to recursively inserting s into the right subtree. In both these cases the recursive call continues searching down the tree looking for the appropriately place to do an insert. - If String s is equal to node.item, we don't need to do anything. This means the String is already in the BST. In fact, we don't even have to explicitly test for this case since we're not going to do anything other than return the node. - Return the node. The way to think about this is that you're returning the subtree rooted at node into which you've inserted the String. Implementing public boolean contains (String s) This method allows you to search through the BST for a specified string, String s. It will return true if the string is stored within the BST, false otherwise. All the work is done by the recursive helper function, recursiveSearch() . All that contains() does is return the result of calling recursiveSearch() with the root and the String as arguments. Implementing protected boolean recursiveSearch (BSTNode node, String s) This helper function searches the subtree rooted at node for the String s, returning true if it finds it, false otherwise. - If node is null we haven't found the String. Return false. - If the item stored in node is equal to s, we've found the string. Return true. - If String s is alphabetically before node.item, return the result of recursively searching the left subtree of node. Implementing protected boolean recursiveSearch (BSTNode node, String s) This helper function searches the subtree rooted at node for the String s, returning true if it finds it, false otherwise. - If node is null we haven't found the String. Return false . - If the item stored in node is equal to s, we've found the string. Return true. - If String s is alphabetically before node.item, return the result of recursively searching the left subtree of node. - If String s is alphabetically after node.item, return the result of recursively searching the right subtree of node. Implementing public void delete (String s) This method searches for String s and deletes the node in the BST containing it. If it does not find the specified string, then the method will do nothing. Implementation of delete( String s) will require the assistance of three helper functions. - protected BSTNode recursiveRemove (BSTNode node, String s) - given a subtree rooted at node and a String s, returns the node that is the root of the new subtree that results from removing s from the subtree. - protected BSTNode deleteNode (BSTNode node) - given a node to remove, returns the new subtree that results from removing that node. This is the method that handles the four cases for deleting nodes: leaf nodes (no children), just a left child, just a right child, and two children (the most complicated case). - protected String getSmallest (BSTNode node) - returns the alphabetically smallest (first in alphabetical order) String in the subtree whose root is the node argument. All delete() does is set the root equal to the result of calling recursiveRemove() with the root and string as arguments. Implementing protected Node recursiveRemove (BSTNode node, String s) This function is somewhat similar to the recursive helper functions for put(). If the node is not equal to null, then we need to compare node.item with the string. Implementing protected boolean recursiveSearch (BSTNode node, String s) This helper function searches the subtree rooted at node for the String s, returning true if it finds it, false otherwise. - If node is null we haven't found the String. Return false . - If the item stored in node is equal to s, we've found the string. Return true. - If String s is alphabetically before node.item, return the result of recursively searching the left subtree of node. - If String s is alphabetically after node.item, return the result of recursively searching the right subtree of node. Implementing public void delete (String s) This method searches for String s and deletes the node in the BST containing it. If it does not find the specified string, then the method will do nothing. Implementation of delete( String s) will require the assistance of three helper functions. - protected BSTNode recursiveRemove (BSTNode node, String s) - given a subtree rooted at node and a String s, returns the node that is the root of the new subtree that results from removing s from the subtree. - protected BSTNode deleteNode (BSTNode node) - given a node to remove, returns the new subtree that results from removing that node. This is the method that handles the four cases for deleting nodes: leaf nodes (no children), just a left child, just a right child, and two children (the most complicated case). - protected String getSmallest (BSTNode node) - returns the alphabetically smallest (first in alphabetical order) String in the subtree whose root is the node argument. All delete() does is set the root equal to the result of calling recursiveRemove() with the root and string as arguments. Implementing protected Node recursiveRemove (BSTNode node, String s) This function is somewhat similar to the recursive helper functions for put(). If the node is not equal to null, then we need to compare node.item with the string. Implementing protected String getSmallest (BSTNode node) To start the process for finding the smallest string in the subtree rooted at node, define a String variable smallest and set it equal to node.item. Now we'll keep on following left branches in the tree (since things to the left are always smaller values), until we can't go left any more. Then we know we've found the smallest value. - While node.left is not null Set smallest equal to node.left.item. Set node equal to node.left. Return smallest. Traversing BSTs (Optional) (Numbers beside nodes indicate traversal order.) In this portion of the assignment, you will be implementing these methods, which enable you to traverse through your BST: public MyQueue inOrder 0 : Does an in-order traversal to return a queue of strings in-order. This is the strings in alphabetical order. public MyQueue preOrder () : Does a pre-order traversal to return a queue of strings pre-order. This is the order in which you'd want to insert the strings into a new tree to replicate the tree structure. public MyQueue postOrder ( ) : Does a post-order traversal to return a queue of strings post-order. This is the order of strings from the leaves upward, starting from the left and going rightward. For examples of how these traversals work and further information, you may visit the following links: https://www.youtube.com/watch?v=gm8DUJJhmY4 https://www.youtube.com/watch?v=5dySuyZf9Qg https://www.tutorialspoint.com/data_structures_algorithms/tree_traversal.htm Each of the functions has a recursive helper function: - void inOrderRecursive (BSTNode node, MyQueue queue) - void preOrderRecursive (BSTNode node, MyQueue queue) - void postOrderRecursive (BSTNode node, MyQueue queue) Implementing public MyQueue inOrder () - Create a new MyQueue . - Call inOrderRecursive() with the root and the new MyQueue as arguments. - Return the MyQueue. Each of the functions has a recursive helper function: - void inOrderRecursive (BSTNode node, MyQueue queue) - void preOrderRecursive (BSTNode node, MyQueue queue) - void postOrderRecursive (BSTNode node, MyQueue queue) Implementing public MyQueue inOrder () - Create a new MyQueue. - Call inOrderRecursive() with the root and the new MyQueue as arguments. - Return the MyQueue. Implementing preOrder() and postOrder() Follow the same pattern. Implementing protected void inOrderRecursive (BSTNode node,MyQueue queue) If the node is not null - Recursively call inOrderRecursive() on the left subtree. - Add node.item to the queue. - Recursively call inOrderRecursive() on the right subtree. Each of the other recursive helpers follow the same pattern. For pre-order, you add to the queue first, then recursively process the left and right subtrees, while for post-order you recursively process the left and right subtrees first, then add the current node.item to the queue at the end