Java Programming Project 3

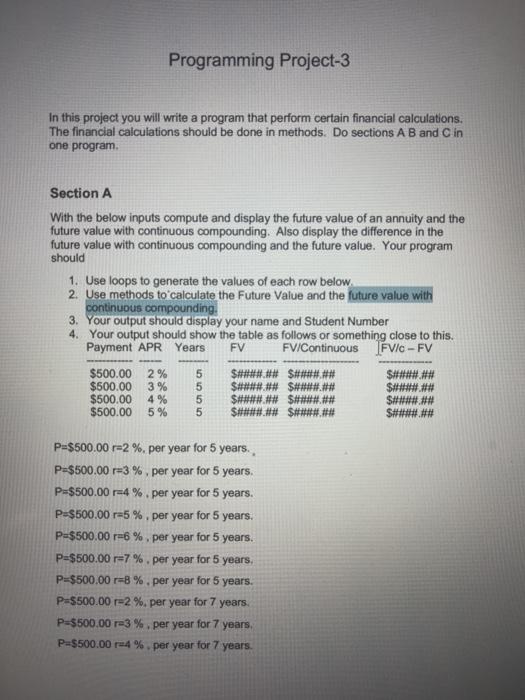
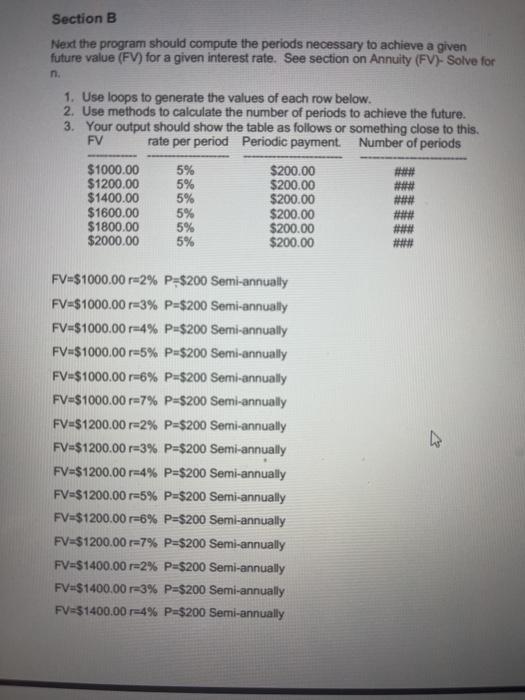
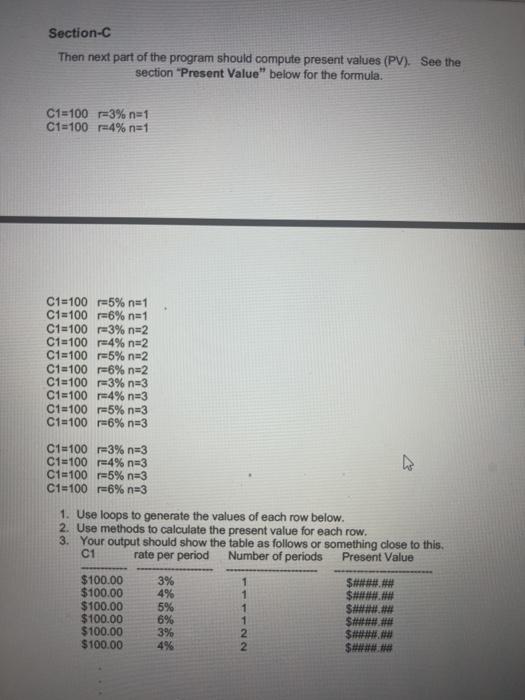
Programming Project-3 In this project you will write a program that perform certain financial calculations. The financial calculations should be done in methods. Do sections A B and Cin one program Section A With the below inputs compute and display the future value of an annuity and the future value with continuous compounding. Also display the difference in the future value with continuous compounding and the future value. Your program should 1. Use loops to generate the values of each row below. 2. Use methods to calculate the Future Value and the future value with continuous compounding. 3. Your output should display your name and Student Number 4. Your output should show the table as follows or something close to this. Payment APR Years FV FV/Continuous FVic - FV $500.00 2% 5 $#**##.## $###### $###### $600.00 3% 5 $####.## $#### $###### $500.00 4 % 5 $####.## $###### S#### $500.00 5% 5 ######### S###### P=$500.00 r=2 %, per year for 5 years.. P=$500.00 r=3 %, per year for 5 years. P=$500.00 -4%. per year for 5 years. P=$500.00 r5%, per year for 5 years. P-$500.00 r=6 %. per year for 5 years. P-$500.00 r=7% per year for 5 years, P=$500.00 r=8 %. per year for 5 years. P=$500.00 -2%. per year for 7 years. P-5500.00 3% per year for 7 years, P=$500.00 4 %. per year for 7 years Section B Next the program should compute the periods necessary to achieve a given future value (FV) for a given interest rate. See section on Annuity (FV)-Solve for n. 1. Use loops to generate the values of each row below. 2. Use methods to calculate the number of periods to achieve the future. 3. Your output should show the table as follows or something close to this. rate per period Periodic payment Number of periods FV $1000.00 $1200.00 $1400.00 $1600.00 $1800.00 $2000.00 5% 5% 5% 5% 5% 5% $200.00 $200.00 $200.00 $200.00 $200.00 $200.00 FV#$1000,00 r=2% P=$200 Semi-annually FV=$1000.00 -3% P=$200 Semi-annually FV=$1000.00 -4% P=$200 Semi-annually FV=$1000.00 r=5% P$200 Semi-annually FV=$1000.00 r=6% P=$200 Semi-annually FV=$1000.00 r=7% P=$200 Semi-annually FV=$1200.00 r-2% P=$200 Semi-annually FV=$1200.00 r=3% P=$200 Semi-annually FV=$1200.00 -4% P=$200 Semi-annually FV=$1200.00 -5% P=$200 Semi-annually FV=$1200.00 r=6% P=$200 Semi-annually FV=$1200.00 r-7% P=$200 Semi-annually FV-S1400.00 r-2% P=$200 Semi-annually FV-$1400.00 r3% P=$200 Semi-annually FV=$1400.00 -4% P=$200 Semi-annually Section-C Then next part of the program should compute present values (PV). See the section Present Value" below for the formula C1=100 =3% na1 C1=100 r4% n=1 C1=100 =5% n=1 C1=100 =6% na 1 C1=100 23% n=2 C1-100 24% n=2 C1=100 =5% n=2 C1-100 =6% n=2 C1-100 =3% n=3 C1100 4% n3 C1-100 E5% n=3 C1-100 =6% n=3 C1-100 =3% n-3 C1-100 4% n=3 C1-100 -5% n=3 C1100 6% n=3 1. Use loops to generate the values of each row below. 2. Use methods to calculate the present value for each row. 3. Your output should show the table as follows or something close to this. C1 rate per period Number of periods Present Value $100.00 3% 1 $####### $100.00 4% 1 $###### $100.00 5% S###### $100.00 6% S###### $100.00 3% $100.00 4% $###### 1 NN- Formulas and Examples FV of Annuity =P P-Periodic Payment Trate per period n-number of periode A ne future value of an annuity formula is used to calculate what e value at a future date would be for a series of periodic yments, the future value of an annuity formula assumes that The rate does not change The first payment is one period away The periodic payment does not change o periodic payment does change ert FVA w/Continuous Comp. = CFX er-1 FVA = Future Value of Annuity OF =Cash Flow Trate t = time The future value (FV) of an annuity with continuous compounding formula is used to calculate the ending balance on a series of periodic payments that are compounded continuously. Understanding the future value of annuity with continuous compounding formula requires the understanding of two specific financial and mathematical concepts, which are future value of an annuity and continuous compounding. Future Value of Annuity, Continuous Compounding, and Geometric Series Future Value of Annuity - The future value of an annuity is the sum of a series of periodic payments and typically involves compounding of interest as the balance increases. The formula for future value of annuity alone generally solves the question "How much will I have said Annuity (FV)- Solve for n neva = In (1+ --. (1+"VX+) +(1 + r) n1 = number of periods FV = Future Value (of Annuity) r=rate P= Payment/Cash Flows The formula for solving for number of periods (n) on an annuity shown above is used to calculate the number of periods based on the future value, rate, and periodic cash flows. The formula above, solving for n, generally approaches the question "How long will it take to save $x amount dollars by saving sy per month at a rate of z%". Example of Solve for n on Annuity Formula Suppose that an individual receives an additional $1000 pay or bonus semiannually. Suppose this individual would like to find out how long until they saye $19600 by saying $1.00 Pery hair Present Value PV = C1 (1+r)" C = Cash Flow at period 1 T= rate of return n = number of periods Present Value (PV) is a formula used in Finance that calculates the present day value of an amount that is received at a future date. The premise of the equation is that there is "time value of money". Time value of money is the concept that receiving something today is worth more than receiving the same item at a future date. The presumption is that it is preferable to receive $100 today than it is to receive the same amount one year from today, but what if the choice is between $100 present day or $106 a year from today? A formula is needed to provide a quantifiable comparison between an amount today and an amount at a future time, in terms of its present day value. Use of Present Value Formula The Present Value formula has a broad range of uses and may be applied to various areas of finance including corporate finance, banking finance, and investment finance. Apart from the various areas of finance that present value analysis is used, the formula is also used as a component of other financial formulas