just help with the highlighted part, thank you.

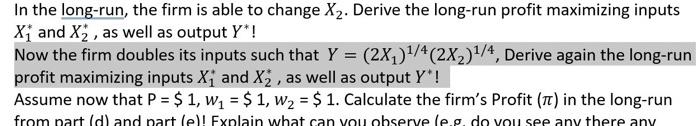
e. Now the firm doubles its inputs such that Y = (2x2)1/4(2x2)1/4, where a and b depend on Your group's initial production function. Derive again the long-run profit maximizing inputs Xi and X; , as well as output Y'! f. Assume now that P = $ 1,w, = $ 1,w2 = $ 1. Calculate the firm's Profit (T) in the long-run from part (d) and part (e)! Explain what can you observe (e.g. do you see any there any difference)! (Note: you are NOT allowed to change P, W7, W2 = $1 in the previous parts (part a until e), this action is only for the purpose of part f question) g. How would you relate your answer in part f with the concept of return to scale & profit, explain! Provide graphical analysis in your explanation with Y on the vertical-axis and X on the horizontal-axis. In the long-run, the firm is able to change X2. Derive the long-run profit maximizing inputs X and X, as well as output Y*! Now the firm doubles its inputs such that Y = (2x2) 1/4 (2X,)1/4, Derive again the long-run profit maximizing inputs X; and X, as well as output Y*! Assume now that P = $ 1, w= $ 1, W2 = $ 1. Calculate the firm's Profit (T) in the long-run from part (d) and part le)! Explain what can you observe leg. do you see any there any e. Now the firm doubles its inputs such that Y = (2x2)1/4(2x2)1/4, where a and b depend on Your group's initial production function. Derive again the long-run profit maximizing inputs Xi and X; , as well as output Y'! f. Assume now that P = $ 1,w, = $ 1,w2 = $ 1. Calculate the firm's Profit (T) in the long-run from part (d) and part (e)! Explain what can you observe (e.g. do you see any there any difference)! (Note: you are NOT allowed to change P, W7, W2 = $1 in the previous parts (part a until e), this action is only for the purpose of part f question) g. How would you relate your answer in part f with the concept of return to scale & profit, explain! Provide graphical analysis in your explanation with Y on the vertical-axis and X on the horizontal-axis. In the long-run, the firm is able to change X2. Derive the long-run profit maximizing inputs X and X, as well as output Y*! Now the firm doubles its inputs such that Y = (2x2) 1/4 (2X,)1/4, Derive again the long-run profit maximizing inputs X; and X, as well as output Y*! Assume now that P = $ 1, w= $ 1, W2 = $ 1. Calculate the firm's Profit (T) in the long-run from part (d) and part le)! Explain what can you observe leg. do you see any there any