Just need help with an easy intro level python in jupyter notebook if possible:

Lab2 Series: Calculate sinh(x)

Calculate sinh(x) two different ways and compare the result with the built-in function. Use the following Taylor series expansion of sinh (as method 1):

sinhx=ex-e-x2= n=0x2n+12n+1!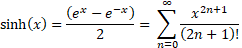

When calculating this series, you will notice that the denominator becomes very large for small values of n. For example, for x=2, the tenth term (n=10) becomes:

22*10+12*10+1!=22121!0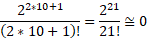

The result is a small number that cant be represented in digital computers because they have a limited number of bits to store them. Rounding errors, overflow and underflow are some of the major causes of computational errors. See Boas Numerical Calculations, pp36. The small errors accumulate when faulty intermediate results are used repeatedly in calculating a series. There are ways to avoid these errors. Here is one way to do that in this case. Instead of calculating each term independently, calculate a new term (n+1) from the previously calculated term (n) in the series. Define a ratio of two adjacent terms T(n+1) and T(n):

rn=(Tn+1)/Tn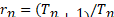

rn=x22n+22n+3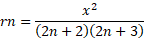

Then the (n+1) th. term becomes:

Tn+1=rn*Tn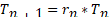

Use this as method two for computing sinh.

Suggested pseudo code:

1. Define N, number of terms to calculate
2. Define x values using linspace(-2,2,10) function
3. Initialize needed variables
4. For each value of x compute sinh with two methods.
   1. For n = 0 to N compute sinh two ways
      1. Compute rn using the equation given above
      2. Compute next term in series, Tn+1= r*Tn
      3. Compute partial sum using method 1
      4. Compute partial sum using method 2
   2. Save sinh values
5. Print or plot results

You can use the following code to plot your results. In this code, x is a vector of x values for which sinh is calculated and S1, S2 are vectors that contain the corresponding sinh values for method 1 and method2 respectively.

%matplotlib inline (this is needed only in Jupyter notebook not Python)

import matplotlib.pyplot as plt

plt.plot(x, S1, x, S2, x, np.sinh(x))

plt.title('Sinh(x) computed two ways')

plt.xlabel('x')

plt.ylabel('sinh(x)')

plt.legend(['S1', 'S2', 'Standard'])

plt.show()