just need the first example with 810 million and 910 million. i attached a similar problem with correct work so i hope that helps. i cant seem to figure it out.

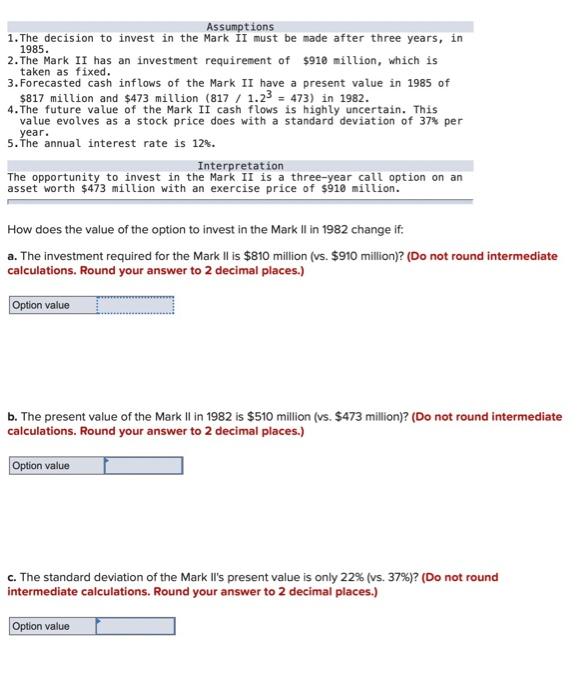
Assumptions 1. The decision to invest in the Mark II must be made after three years, in 1985. 2. The Mark II has an investment requirement of $910 million, which is taken as fixed. 3. Forecasted cash inflows of the Mark II have a present value in 1985 of $817million and $473million(817/1.23=473) in 1982. 4. The future value of the Mark II cash flows is highly uncertain. This value evolves as a stock price does with a standard deviation of 37% per year. 5. The annual interest rate is 12%. How does the value of the option to invest in the Mark II in 1982 change if: a. The investment required for the Mark II is $810 milion (vs. $910 million)? (Do not round intermediate calculations. Round your answer to 2 decimal places.) b. The present value of the Mark II in 1982 is $510 million (v5. $473 million)? (Do not round intermediate calculations. Round your answer to 2 decimal places.) c. The standard deviation of the Mark Il's present value is only 22% (vs. 37\%)? (Do not round intermediate calculations. Round your answer to 2 decimal places.) 1. The decision to invest in the Mark II must be made after three years, in 1985. 2. The Mark II has an investment requirement of $975 million, which is taken as fixed. 3. Forecasted cash inflows of the Mark II have a present value in 1985 of $882million and $510million(882/1.23=510) in 1982 . 4. The future value of the Mark II cash flows is highty uncertain. This value evolves as a stock price does with a standard deviation of 394 per year. 5. The annual interest rate is 10%. How does the value of the option to invest in the Mark II in 1982 change if: a. The investment required for the Mark II is $875 million (vs. $975 million)? (Do not round intermediate calculations. Round your answer to 2 decimal places.) b. The present value of the Mark II in 1982 is $575 million (vs. $510 million)? (Do not round intermediate calculations. Round your answer to 2 decimal places.) c. The standard deviation of the Mark Il's present value is only 24% (vs. 39\%)? (Do not round intermediate calculations. Round your answer to 2 decimal places.) Explanation a. =510;EX=875;=0.39;t=3.0rf=0.10 d1=log[PrPV(EX)]/t+t/2d1=log(5109(875/1.105)/(0.393.0)+(0.393.0)2=0.0381d2=d1t=0.0381(0.39350)=0.7136N(d1)=N(6.0381)N(d1)=0.4848N(d2)=N(6,7136)N(d2)=0.2377Callvalue=[N(d1)P][N(d2)PV(EX)]Callvalue=[0.4848510][0.2377(875/1.103)]Callvalue=$90.96 b. P=575;EX=975;=0.39;t=3.0rf=8.18d1=log[P/PV(EX)]t+at/2d1=log[575/(975/1.103)y(0.393.0)+(0.393.0)=0.0307d2=d1t=0.0207(0.393.0)=0.6962N(d1)=N(6.6207)N(d1)=0.4917N(d2)=N(8.6962)N(d2)=0.2431Callvalue=[N(d1)P][N(d2)PV(EX)]Callvalue=[0.4917575][0.2431(975/1.103)]Callvalue=$104.64c.P=510;EX=975;=0.24;t=3.0rf=0.10d1=log[P/PV(EX)]r+t/2d1=log[510(975/1.103)](0.243.0)+(0.243.0)/2=0.6632d2=d1t=0.6632(0.243.0)=1.0789 N(d1)=N(0.6632)N(d1)=0.2536N(d2)=N(1.0789)N(d2)=0.1403Callvalue=[N(d1)P][N(d2)PV(EX)]Callvalue=[0.2536510][0.1403(975/1.103)]Callvalue=$26.55 Assumptions 1. The decision to invest in the Mark II must be made after three years, in 1985. 2. The Mark II has an investment requirement of $910 million, which is taken as fixed. 3. Forecasted cash inflows of the Mark II have a present value in 1985 of $817million and $473million(817/1.23=473) in 1982. 4. The future value of the Mark II cash flows is highly uncertain. This value evolves as a stock price does with a standard deviation of 37% per year. 5. The annual interest rate is 12%. How does the value of the option to invest in the Mark II in 1982 change if: a. The investment required for the Mark II is $810 milion (vs. $910 million)? (Do not round intermediate calculations. Round your answer to 2 decimal places.) b. The present value of the Mark II in 1982 is $510 million (v5. $473 million)? (Do not round intermediate calculations. Round your answer to 2 decimal places.) c. The standard deviation of the Mark Il's present value is only 22% (vs. 37\%)? (Do not round intermediate calculations. Round your answer to 2 decimal places.) 1. The decision to invest in the Mark II must be made after three years, in 1985. 2. The Mark II has an investment requirement of $975 million, which is taken as fixed. 3. Forecasted cash inflows of the Mark II have a present value in 1985 of $882million and $510million(882/1.23=510) in 1982 . 4. The future value of the Mark II cash flows is highty uncertain. This value evolves as a stock price does with a standard deviation of 394 per year. 5. The annual interest rate is 10%. How does the value of the option to invest in the Mark II in 1982 change if: a. The investment required for the Mark II is $875 million (vs. $975 million)? (Do not round intermediate calculations. Round your answer to 2 decimal places.) b. The present value of the Mark II in 1982 is $575 million (vs. $510 million)? (Do not round intermediate calculations. Round your answer to 2 decimal places.) c. The standard deviation of the Mark Il's present value is only 24% (vs. 39\%)? (Do not round intermediate calculations. Round your answer to 2 decimal places.) Explanation a. =510;EX=875;=0.39;t=3.0rf=0.10 d1=log[PrPV(EX)]/t+t/2d1=log(5109(875/1.105)/(0.393.0)+(0.393.0)2=0.0381d2=d1t=0.0381(0.39350)=0.7136N(d1)=N(6.0381)N(d1)=0.4848N(d2)=N(6,7136)N(d2)=0.2377Callvalue=[N(d1)P][N(d2)PV(EX)]Callvalue=[0.4848510][0.2377(875/1.103)]Callvalue=$90.96 b. P=575;EX=975;=0.39;t=3.0rf=8.18d1=log[P/PV(EX)]t+at/2d1=log[575/(975/1.103)y(0.393.0)+(0.393.0)=0.0307d2=d1t=0.0207(0.393.0)=0.6962N(d1)=N(6.6207)N(d1)=0.4917N(d2)=N(8.6962)N(d2)=0.2431Callvalue=[N(d1)P][N(d2)PV(EX)]Callvalue=[0.4917575][0.2431(975/1.103)]Callvalue=$104.64c.P=510;EX=975;=0.24;t=3.0rf=0.10d1=log[P/PV(EX)]r+t/2d1=log[510(975/1.103)](0.243.0)+(0.243.0)/2=0.6632d2=d1t=0.6632(0.243.0)=1.0789 N(d1)=N(0.6632)N(d1)=0.2536N(d2)=N(1.0789)N(d2)=0.1403Callvalue=[N(d1)P][N(d2)PV(EX)]Callvalue=[0.2536510][0.1403(975/1.103)]Callvalue=$26.55