$k_1=20\frac{N}{m},k_2=30\frac{N}{m},k_3=30\frac{N}{m},m_1=m_2=20kg,$

$y_1(0)=y_2(0)=0,y_1^{\text{'}}(0)=2\frac{m}{s}$ and $y_2^{\text{'}}(0)=-1\frac{m}{s}$

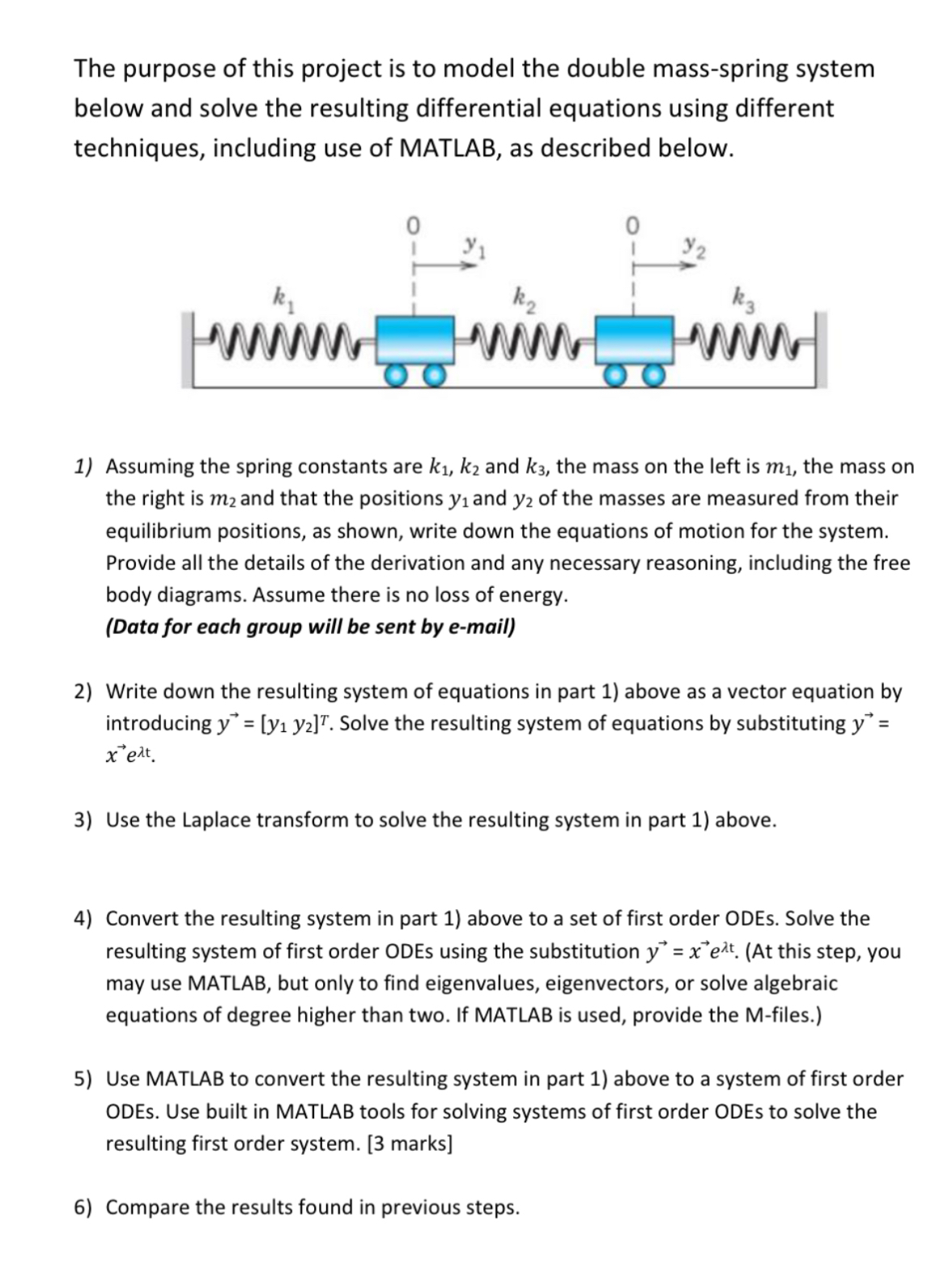
The purpose of this project is to model the double mass$-$spring system below and solve the resulting differential equations using different techniques, including use of MATLAB, as described below.

Assuming the spring constants are $k_1,k_2$ and $k_3,$ the mass on the left is $m_1,$ the mass on the right is $m_2$ and that the positions $y_1$ and $y_2$ of the masses are measured from their equilibrium positions, as shown, write down the equations of motion for the system. Provide all the details of the derivation and any necessary reasoning, including the free body diagrams. Assume there is no loss of energy.

$($Data for each group will be sent by e$-$mail$)$

Write down the resulting system of equations in part $1)$ above as a vector equation by introducing yvec$(y)={\left[\begin{array}{cc}{y}_1& y_2\end{array}\right]}^T.$ Solve the resulting system of equations by substituting vec$(y^{\text{'}})=$ vec$(x)e^t.$

Use the Laplace transform to solve the resulting system in part $1)$ above.

Convert the resulting system in part $1)$ above to a set of first order ODEs. Solve the resulting system of first order ODEs using the substitution vec$(y)=$vec$(x)e^t.($At this step, you may use MATLAB, but only to find eigenvalues, eigenvectors, or solve algebraic equations of degree higher than two. If MATLAB is used, provide the M$-$files.$)$

Use MATLAB to convert the resulting system in part $1)$ above to a system of first order ODEs. Use built in MATLAB tools for solving systems of first order ODEs to solve the resulting first order system. $[3$ marks$]$

Compare the results found in previous steps.