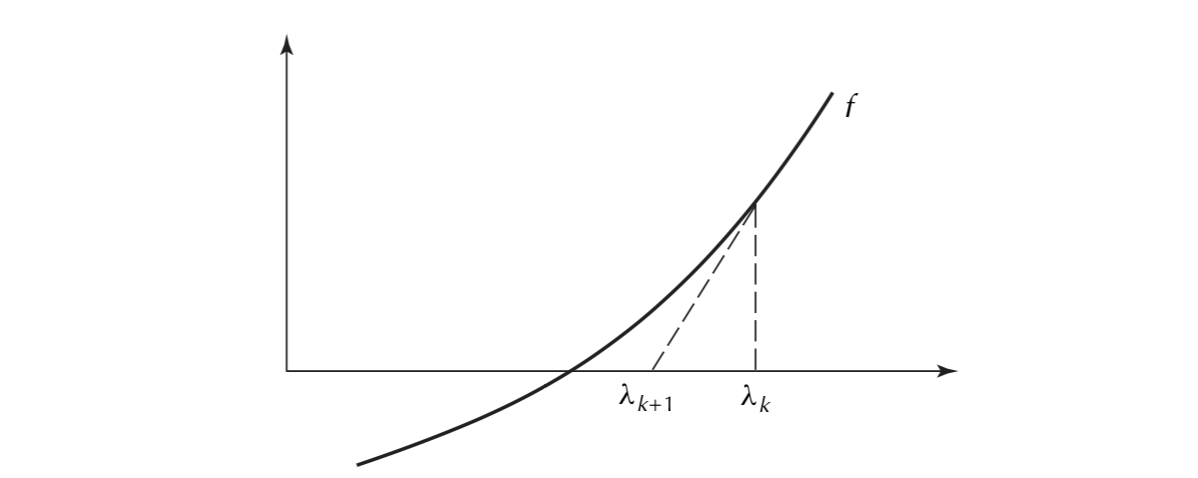
k+1 , 4. (Newton's method o) The IRR is generally calculated using an iterative procedure. Sup- pose that we define f(a) = -20 +aja + a222 + +ana", where all ai's are positive and n > 1. Here is an iterative technique that generates a sequence 10,11,12,..., dk... of estimates that converges to the root > 0, solving f) = 0. Start with any lo > 0 close to the solution. Assuming ik has been calculated, evaluate f'(ak) = a1 +2a21k + 3azk + ... +nanama n-1 and define f(ak) ak+1 = 1k f'(a) This is Newton's method. It is based on approximating the function f by a line tangent to its graph at ik, as shown in Figure 2.4. Try the procedure on f(2)=-1+1+22. Start with 10 = 1 and compute four additional estimates. k+1 , 4. (Newton's method o) The IRR is generally calculated using an iterative procedure. Sup- pose that we define f(a) = -20 +aja + a222 + +ana", where all ai's are positive and n > 1. Here is an iterative technique that generates a sequence 10,11,12,..., dk... of estimates that converges to the root > 0, solving f) = 0. Start with any lo > 0 close to the solution. Assuming ik has been calculated, evaluate f'(ak) = a1 +2a21k + 3azk + ... +nanama n-1 and define f(ak) ak+1 = 1k f'(a) This is Newton's method. It is based on approximating the function f by a line tangent to its graph at ik, as shown in Figure 2.4. Try the procedure on f(2)=-1+1+22. Start with 10 = 1 and compute four additional estimates