key is 59

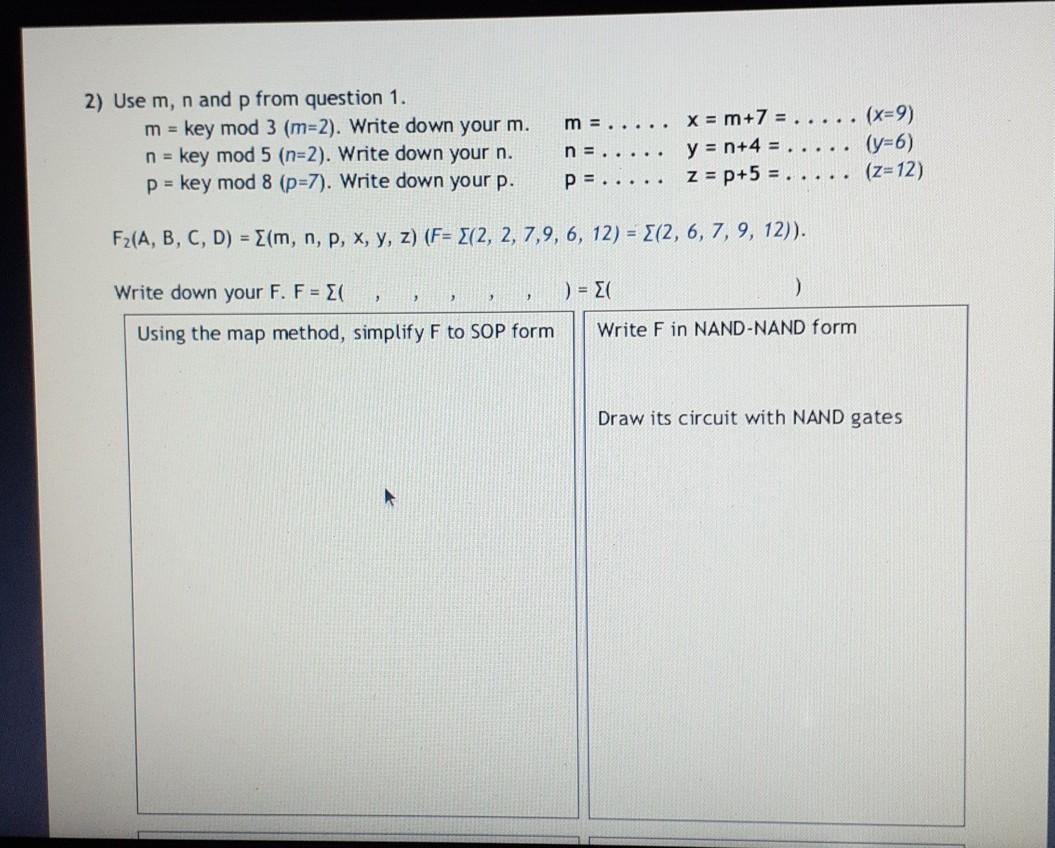
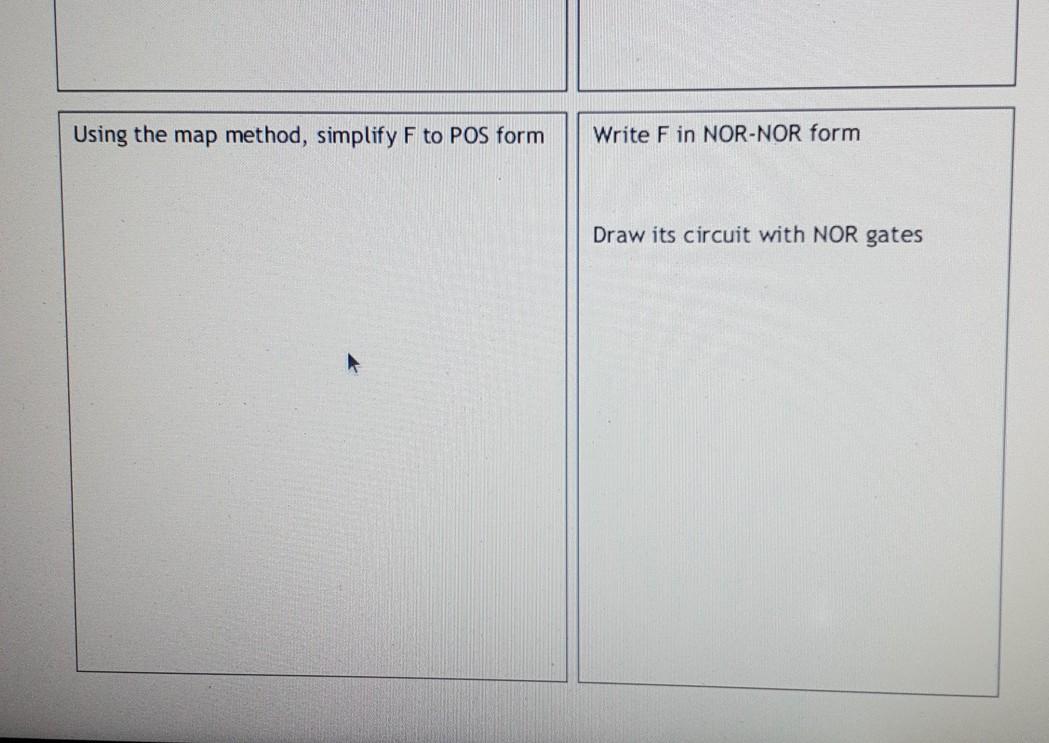
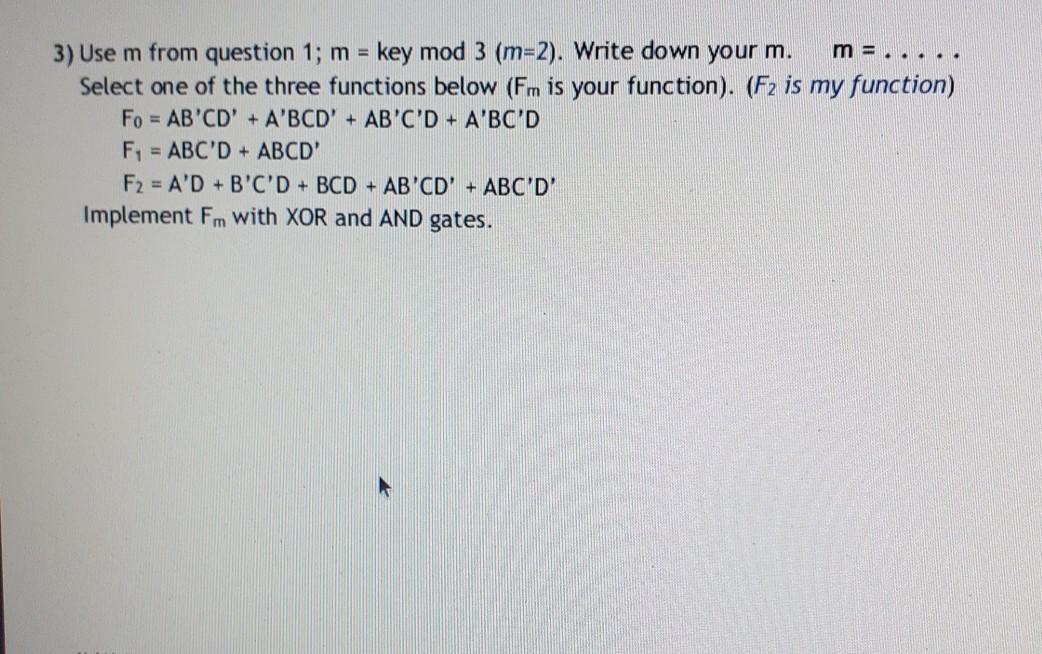
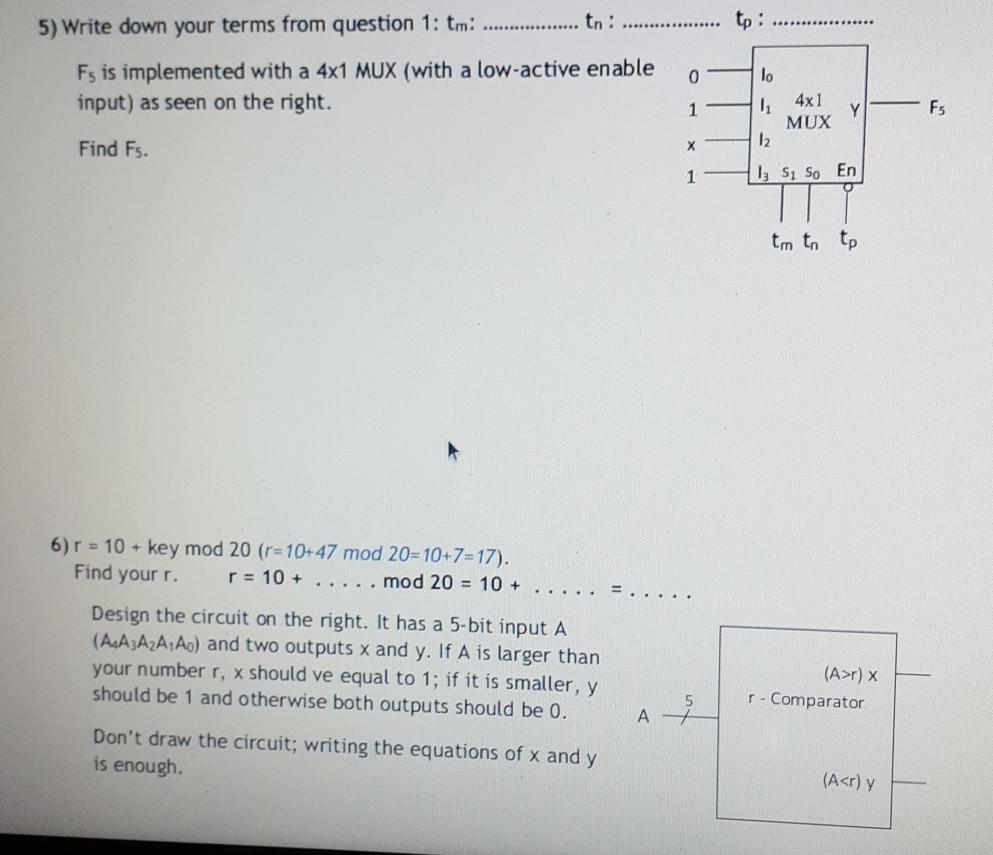
CSE221 - 2020 Fall - Homework 3.pdf Signature: Name: Student Id: CSE 221 - Principles of Logic Design - 2020 Fall Homework 3 You will use a "key" to solve the questions in this homework. The key is the number formed by the last two digits of your student id. If your key is less than 20, add 20 to it! (So for example, if your student id was 20100702047 your key would be "47"; if your student id was 20100702008 your key would be "28".) We will assume that the key is 47 while explaining the questions (you should replace it with your own key). So, first write down your id and key: Student Id: .... Key: 1) Some terms are listed in the table below. Term Term # Term Term Term # Term # Term # Term 12 x+y 8 4 x'+y'+z 0 (to) 2 13 x+z 9 x+y+z' 1 XZ x'yz 5 10 x+y'+z' 14 y+z YZ 2 xyz' 6 11 15 x+y+z x+y' 7 x'y 3 x'yz' m = key mod 3 (m=47 mod 3=2). Find your m. m = . . . . . mod 3 = ..... n = key mod 5 (n=47 mod 5=2). Find your n. n = . . . . . mod 5 = p = key mod 8 (p=47 mod 8=7). Find your p. p= ..... mod 8 = .... F1 = tm + tn + tp (F1 = [2+ t2+ t7=xyz+xy) Find your F1. F1 = t. + tu + t = Using algebraic methods, find the minterms of this function; then list the minterms in minterm shorthand form ( (...)) and using any method write the function in product of maxterms form (F = (x+y'+z) (x+y+z') ...). .. (x=9) 2) Use m, n and p from question 1. m = key mod 3 (m=2). Write down your m. n = key mod 5 (n=2). Write down your n. p = key mod 8 (p=7). Write down your p. m = ..... x = m+7 = y = n+4 = p= ..... z = p+5 = . n = .... (y=6) (z=12) Fz(A, B, C, D) = {(m, n, p, x, y, z) (F= {(2, 2, 7,9,6, 12) = {(2, 6, 7, 9, 12)). Write down your F. F = { 1) = El ) ?? Using the map method, simplify F to SOP form Write F in NAND-NAND form Draw its circuit with NAND gates Using the map method, simplify F to POS form Write F in NOR-NOR form Draw its circuit with NOR gates m =..... 3) Use m from question 1; m = key mod 3 (m=2). Write down your m. Select one of the three functions below (Fm is your function). (Fz is my function) Fo = AB'CD' + A'BCD' + AB'C'D + A'BC'D F1 = ABC'D + ABCD' F2 = A'D + B'C'D + BCD + AB'CD' + ABC'D' Implement Fm with XOR and AND gates. 4) Write down your function in question 1. (F, = xyz'+xy) F1 = Implement F1 using a high-active 3x8 Decoder. Implement F1 using a low-active 3x8 Decoder. Implement F1 using an 8x1 Multiplexer. Implement F, using a 4x1 Multiplexer. tp: 5) Write down your terms from question 1: tm: tn : Fs is implemented with a 4x1 MUX (with a low-active enable input) as seen on the right. 0 lo 1 4x1 MUX Y Fs 12 Find Fs. 1 13 S1 So En TT T tm to tp 6) r = 10 + key mod 20 (r=10+47 mod 20=10+7=17). Find your r. r = 10 + ..... mod 20 = 10 + Design the circuit on the right. It has a 5-bit input A (A.A3A2A, Ao) and two outputs x and y. If A is larger than your number r, x should ve equal to 1; if it is smaller, y should be 1 and otherwise both outputs should be 0. (A>r) x r - Comparator A Don't draw the circuit; writing the equations of x and y is enough (A