Kindly, code the following using C

(

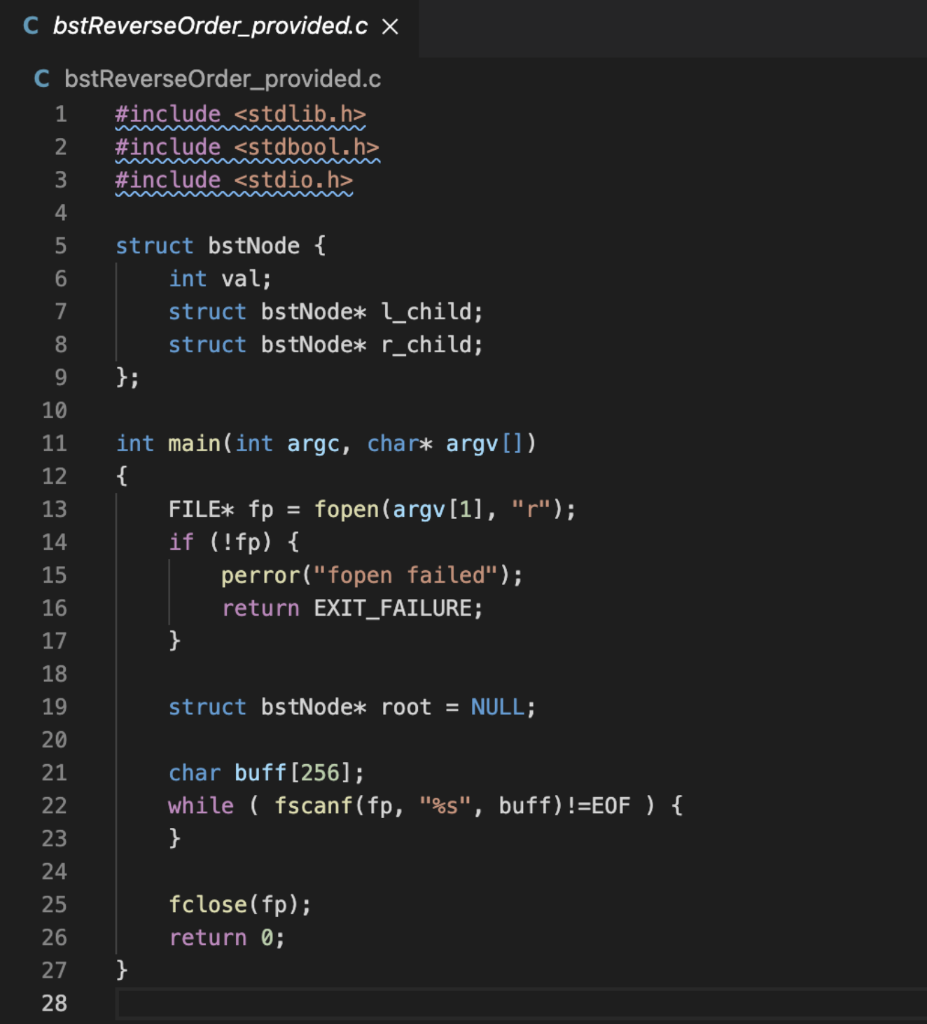
(Skeleton Code)^

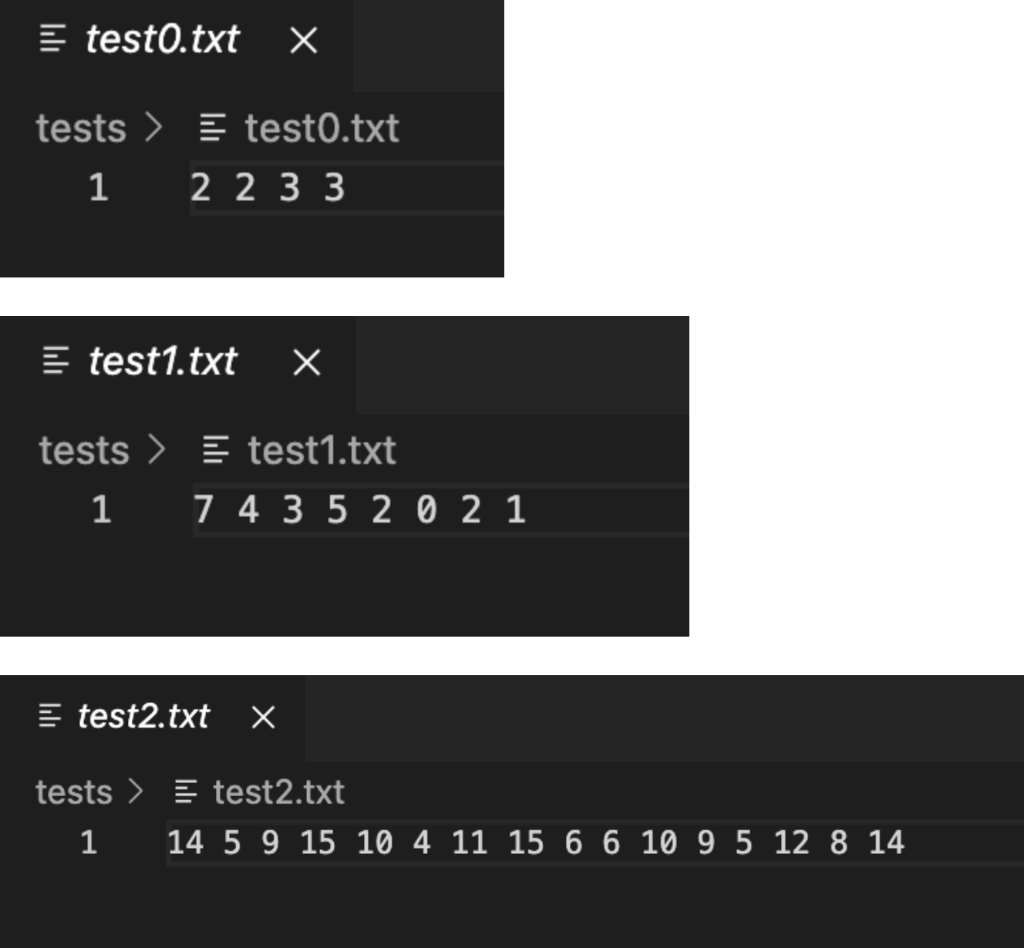
(A few test cases)^

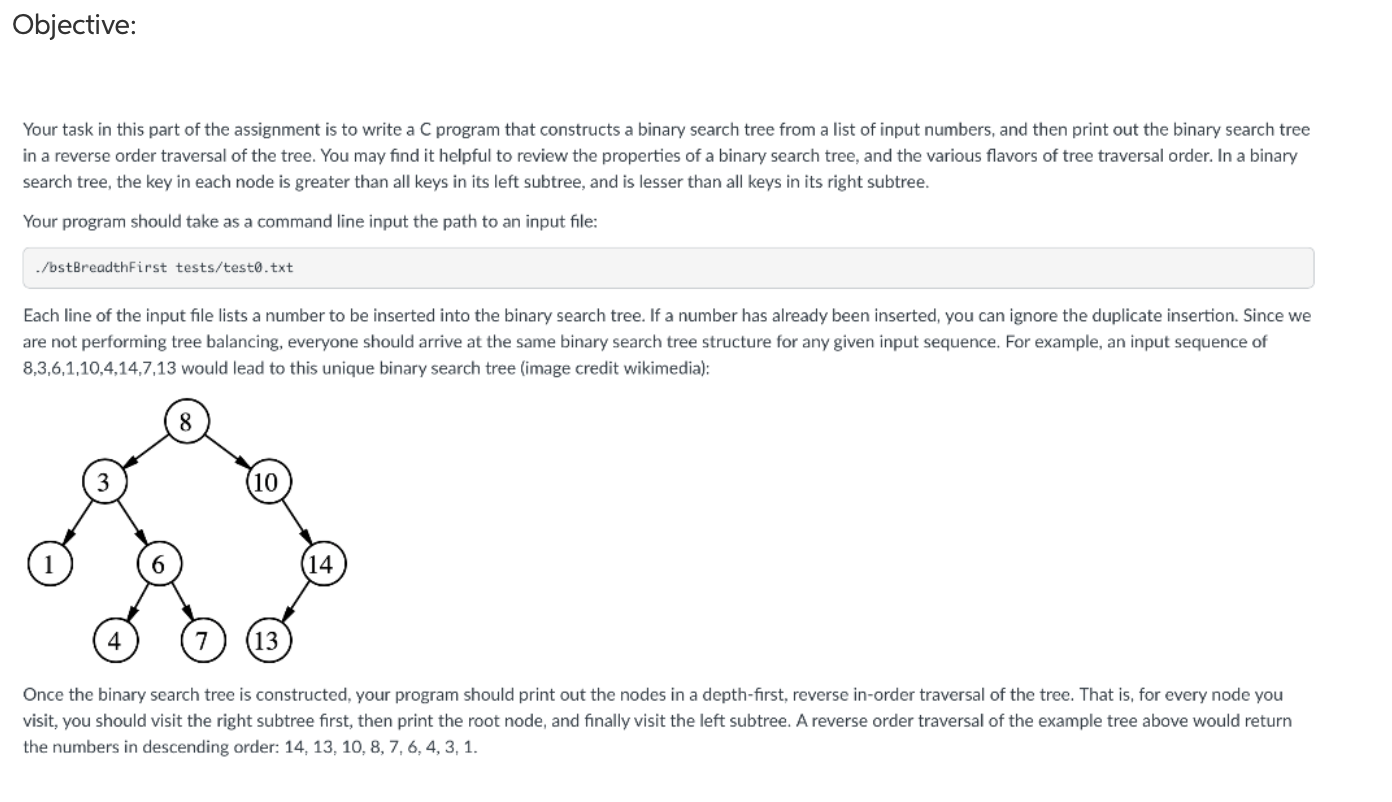(Directions)^

C bstReverse Order_provided.c X C bstReverseOrder_provided.c 1 #include 2 #include 3 #include 4 5 struct bstNode { 6 int val; 7 struct bstNode* l_child; 8 struct bstNode* r_child; 9 }; 10 11 int main(int argc, char* argv[]). 12 13 FILE* fp = fopen (argv[1], "r"); 14 if (!fp) { 15 perror("fopen failed"); 16 return EXIT_FAILURE; 17 } 18 19 struct bstNode* root = NULL; 20 char buff[256]; 22 while ( fscanf(fp,"%s", buff)!=EOF ) { 23 } 24 25 fclose(fp); 26 return 0; 27 } 28 21 testo.txt X tests > testo.txt 1 2 2 3 3 test1.txt tests ) test1.txt 1 7 4 3 5 2 0 2 1 test2.txt tests ) test2.txt 1 14 5 9 15 10 4 11 15 6 6 10 9 5 12 8 14 Objective: Your task in this part of the assignment is to write a C program that constructs a binary search tree from a list of input numbers, and then print out the binary search tree in a reverse order traversal of the tree. You may find it helpful to review the properties of a binary search tree, and the various flavors of tree traversal order. In a binary search tree, the key in each node is greater than all keys in its left subtree, and is lesser than all keys in its right subtree. Your program should take as a command line input the path to an input file: ./bstBreadthFirst tests/test.txt Each line of the input file lists a number to be inserted into the binary search tree. If a number has already been inserted, you can ignore the duplicate insertion. Since we are not performing tree balancing, everyone should arrive at the same binary search tree structure for any given input sequence. For example, an input sequence of 8,3,6,1,10,4,14,7,13 would lead to this unique binary search tree (image credit wikimedia): 10 14 4 (13 Once the binary search tree is constructed, your program should print out the nodes in a depth-first, reverse in order traversal of the tree. That is, for every node you visit, you should visit the right subtree first, then print the root node, and finally visit the left subtree. A reverse order traversal of the example tree above would return the numbers in descending order: 14, 13, 10, 8, 7, 6, 4, 3, 1