Kindly solve the problem

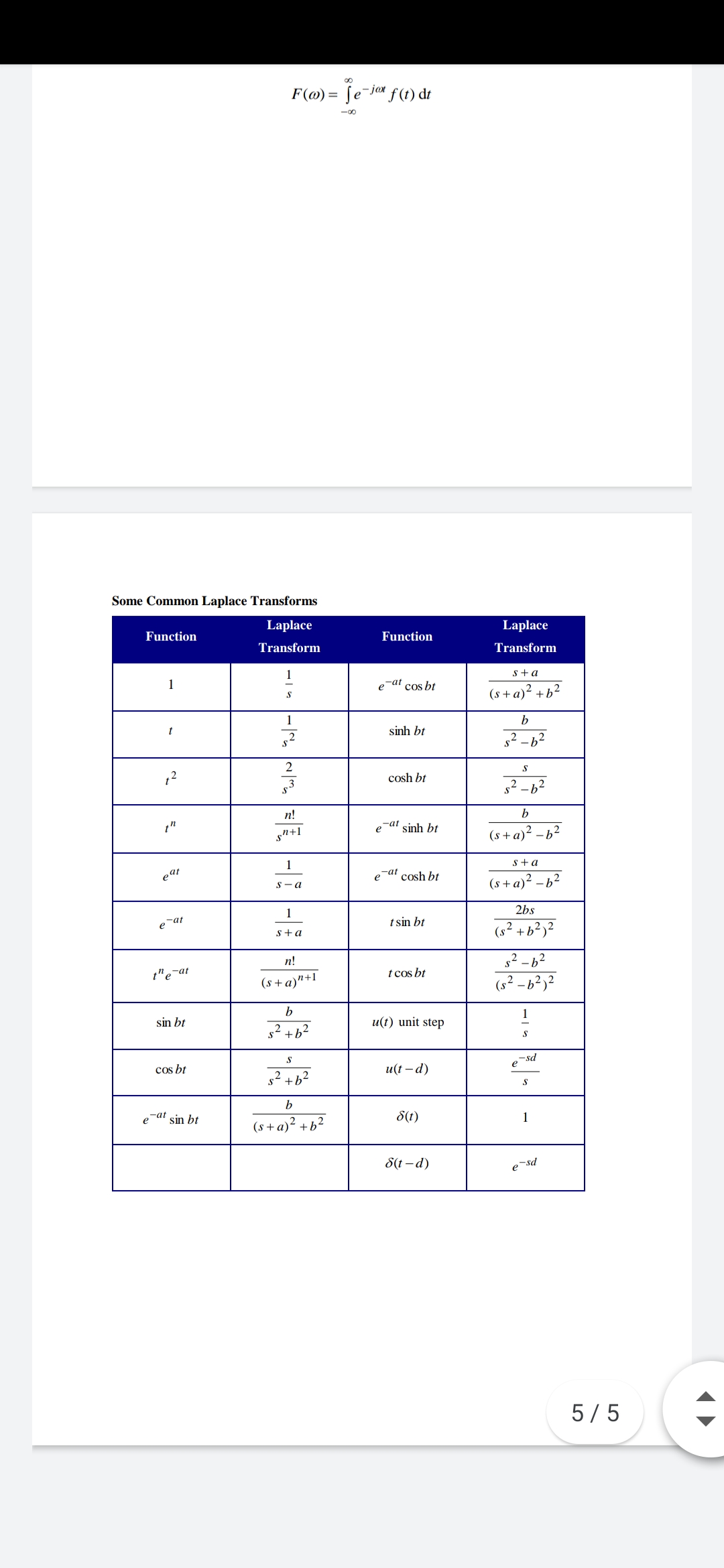
a) A function f (t) = e-at is defined for a > 0 and t > 0. By finding the Fourier transform show that making the substitution s = jw in the Laplace transform of f results in the Fourier transform. The Laplace transform can be taken from the table. (8 marks) b) Show that the Fourier transform of the function f (t ) = 13 - 2Sts2 otherwise is given by 6sin2w F(W) = w (12 marks) c) Use the first shift theorem to find the Fourier transform of g (t) = e-itf(t) (5 marks) INFORMATION The Laplace Transform Let f be a function f(t), for t 2 0. The Laplace transform of this function is then f (s ) = few f ( t ) at Transform Theorem One - The Shift Theorem Let f(t), for t 2 0, be a known function with well defined Laplace transform; given by f (s ) = fe-" f (1 ) at . Let g(t) be a second function formed from the first by multiplying it by e- at: 8 (1) = e a f(t). The transform of g(1) = e"a f(1) is then given by 8 ( s ) = f ( s + a ) . Transform Theorem Two - Powers of t Let f be a function f(t), for t 2 0, with a well defined transform f (s ) = Je -" f ( 1 ) dt .3:44 f 4.00 KB/S Signals and Tran... Q . . . f ( s ) = je -" f ( 1 ) de . Let g(1) be a second function formed from the first by multiplying it by e- at: g (t) = e- at f(1). The transform of g(1) = e"a f(t) is then given by 8 (s ) = f (s+ a ) . Transform Theorem Two - Powers of t Let f be a function f(t), for t 2 0, with a well defined transform f ( s ) = Je-" f ( 1 ) dt . Let g(t) be a second function formed from the first by multiplying it by ?": 8(1) = 1"f(1). The transform of g(1) = 1"f(1) is then given by 8 (s) = (-1)" " f (s ) . The Convolution Theorem Let f(t) and g(t) be two piecewise continuous functions. The convolution of f(t) and g(1), denoted by (f * g)(1), is defined by (f * 8 ) (1) = [f(-v)8(v)dv Laplace Transform and Differential Equations Let f(t) be a function whose Laplace transform is well defined. For a function f, let the symbol Lif} denote its Laplace transform. Then: L(f ') = SL(f) - f(0). The Fourier Transform Let f be a function f(t), for 1 2 0. The Fourier transform of this function is then F(w) = Je-jax f (t) at O O E\f