Knapsack problem / relaxation & bounds

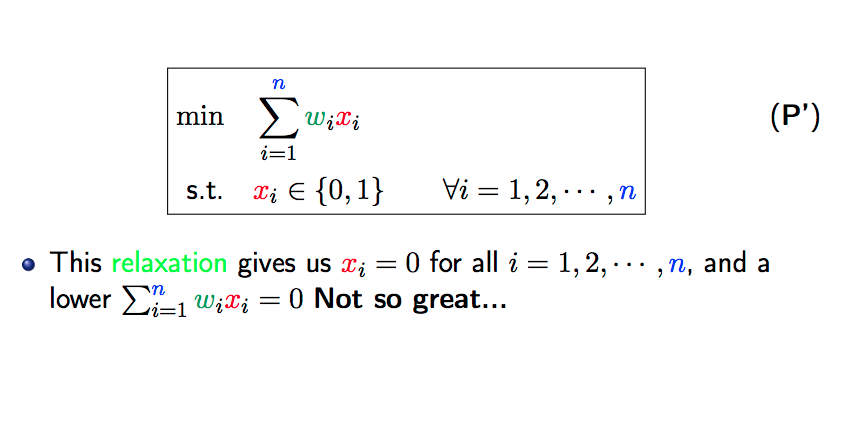
At a flea market in Rome, you spot an. objects (old pictures, a vessel, rusty medals...) that you could resell in your antique shop for double the price. 0 You want these objects to pay for your flight ticket to Rome, which cost 0. 0 Also, your backpack can carry all of them, but you don't want it heavy, so you want to buy the objects that will load your backpack as little as possible. How do you solve this problem? Knapsac p 0 Each object 2' = 1,2, . . . ,n has a price p,- > 0 and a weight w,- > 0. 0 Variables: one variable x,- for each 2' = 1,2,. . . , n. 0 ac,- is a \"yeso" variable: either you take the ith object (m,- : 1) or you do not (m,- : 0). o Constraint: total profit must be at least C 0 As you'll double the price when selling them at your store, the profit for each object is exactly 30,-. 0 Objective Function: the total weight o Nonconvex! 0 Can we come up with a that is easier to solve? n min Wili (P') i=1 s.t. ci E {0,1} Vi = 1,2, . .. , n . This relaxation gives us xi = 0 for all i = 1, 2, . .. , n, and a lower ; with = 0 Not so great...(P") o By integrality we admit fractions of objects. 0 Does this make sense? It is a , and it gives a lower bound. 0 Suppose there are n = 9 objects and C = 70. i123456789 pi2724835298311812 w,- 3 2 2 4 5 4 3 1 4 o P': lower bound is 0. solution is (0. 0. 0. 0. 0. 0. 0. 0. 0). o P": lower bound is 5.71, solution is (0. 1. 0. 0. 0, 0.903, 1, 0). o A upper bound is 8. solution is (1, 1, 1, 0. 0. 0. 0. 1. 0). n 5.71 g ngm: g 8 i=1 0 The global optimum (will learn how to find) is 6. solution is (o, 1, o, o, o, o, 1, 1, o). (12 points) Relaxation 85 Bounds: Consider the knapsack problem similar to the one described in our lecture notes. 8.1]. 23:1301'173' 2 C :13,- 6 {0,1} V15 2 1,2,...,n Suppose that there are 9 objects (n = 9) and that C = 50. 2' 1 2 3 4 5 6 7 8 9 p,- 15 2510 2131 9 1419 29 1a,; 1212 513 3 4 (a) (4 points) Apply the greedy method (by ordering the variables according to their price/weight ratio) to solve the LP relaxation of this problem (where 33,; 6 {0,1} Vi = 1,2,. .. ,n is relaxed to 0