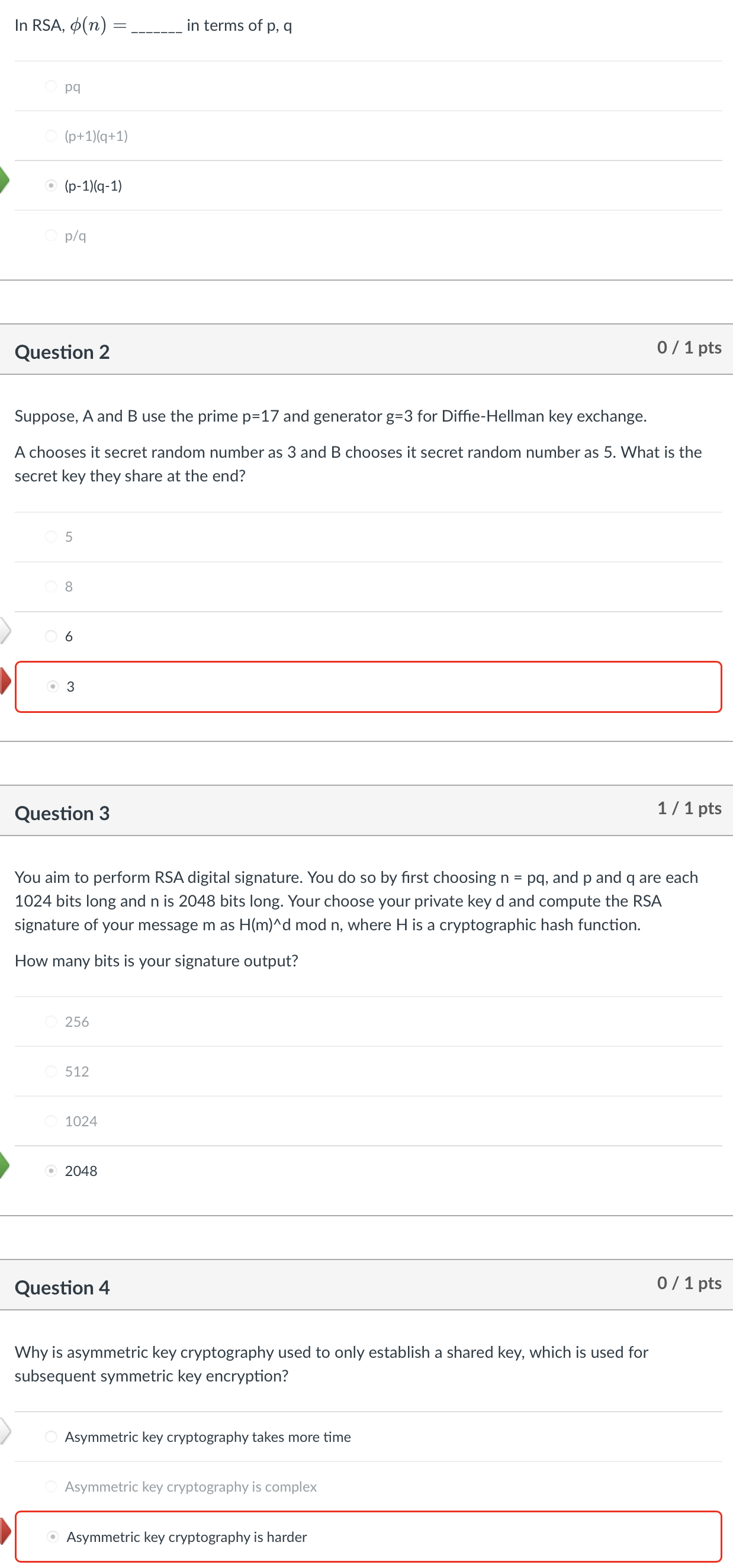
$lnRSA,(n)=$

in terms of $p,q$

$pq$

$(p+1)(q+1)$

$(p-1)(q-1)$

$\frac{p}{q}$

Question $2$

Suppose, A and $B$ use the prime $p=17$ and generator $g=3$ for Diffie$-$Hellman key exchange.

A chooses it secret random number as $3$ and $B$ chooses it secret random number as $5.$ What is the

secret key they share at the end?

$5$

$8$

$6$

$3$

Question $3$

You aim to perform RSA digital signature. You do so by first choosing $n=pq,$ and $p$ and $q$ are each

$1024$ bits long and $n$ is $2048$ bits long. Your choose your private key $d$ and compute the RSA

signature of your message $m$ as $H(m{)}^d$ mod $n,$ where $H$ is a cryptographic hash function.

How many bits is your signature output?

$256$

$512$

$1024$

$2048$

Question $4$

Why is asymmetric key cryptography used to only establish a shared key, which is used for

subsequent symmetric key encryption?

Asymmetric key cryptography takes more time

Asymmetric key cryptography is complex