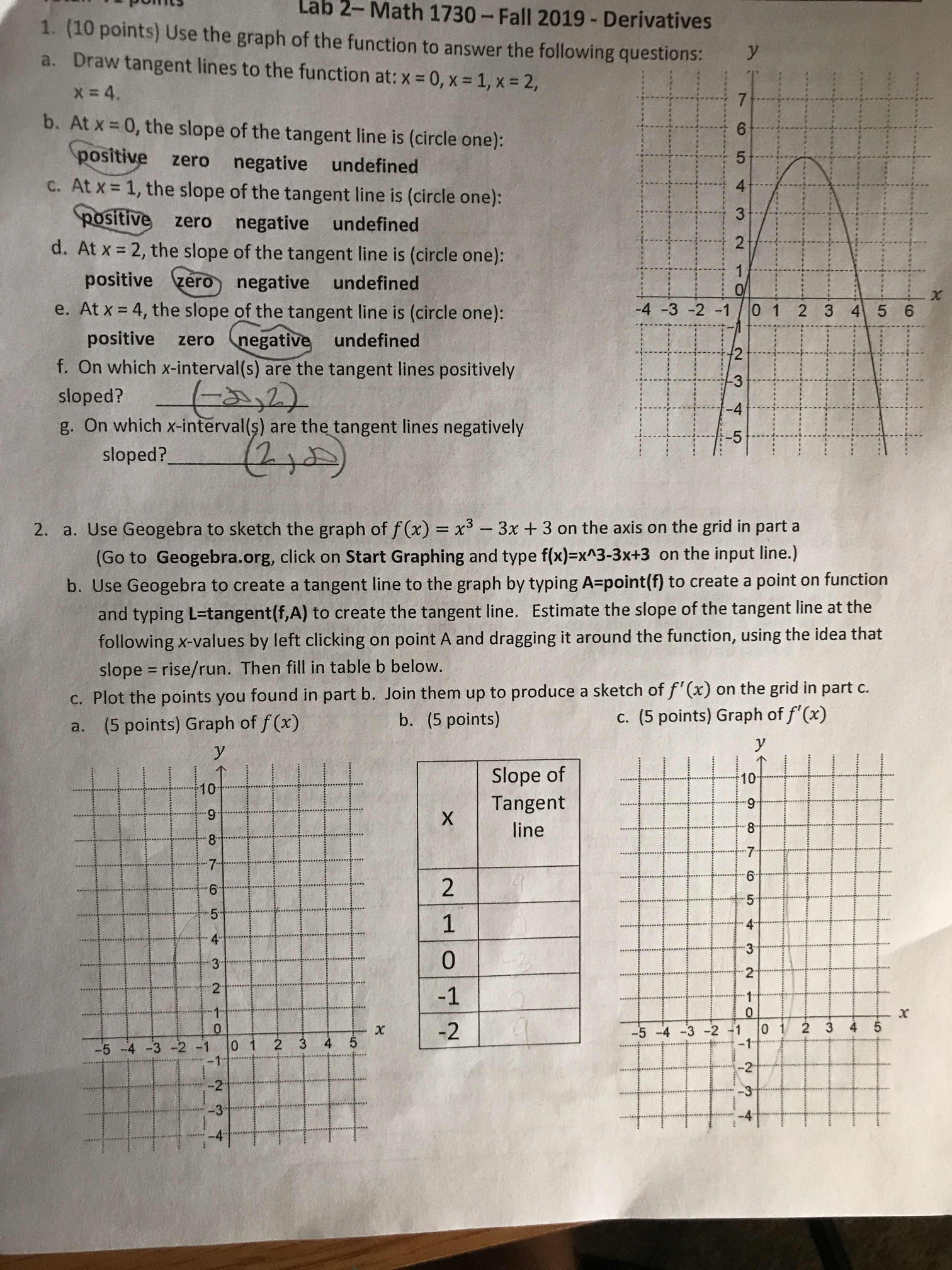
Lab 2- Math 1730 - Fall 2019 - Derivatives 1. (10 points) Use the graph of the function to answer the following questions: a. Draw tangent lines to the function at: x = 0, x = 1, x = 2, X = 4. b. At x = 0, the slope of the tangent line is (circle one): 6 positive zero negative undefined C. At x = 1, the slope of the tangent line is (circle one): positive zero negative undefined d. At x = 2, the slope of the tangent line is (circle one): N W positive zero) negative undefined e. At x = 4, the slope of the tangent line is (circle one): 4 -3 -2 -1 01 2 3 4 5 6 positive zero (negative undefined f. On which x-interval(s) are the tangent lines positively sloped? ( - 2 , 2 ) g. On which x-interval(s) are the tangent lines negatively sloped? 2. a. Use Geogebra to sketch the graph of f(x) = x3 - 3x + 3 on the axis on the grid in part a (Go to Geogebra.org, click on Start Graphing and type f(x)=x^3-3x+3 on the input line.) b. Use Geogebra to create a tangent line to the graph by typing A=point(f) to create a point on function and typing L=tangent(f,A) to create the tangent line. Estimate the slope of the tangent line at the following x-values by left clicking on point A and dragging it around the function, using the idea that slope = rise/run. Then fill in table b below. c. Plot the points you found in part b. Join them up to produce a sketch of f'(x) on the grid in part c. a. (5 points) Graph of f (x) b. (5 points) c. (5 points) Graph of f'(x) Slope of X Tangent line 2 O -1 -5 -4 -3 -2 -1 01 2 3 4 5 -2 O - NW AU O NO 6 0 1-3 -2 1 01 23 5 X X -5