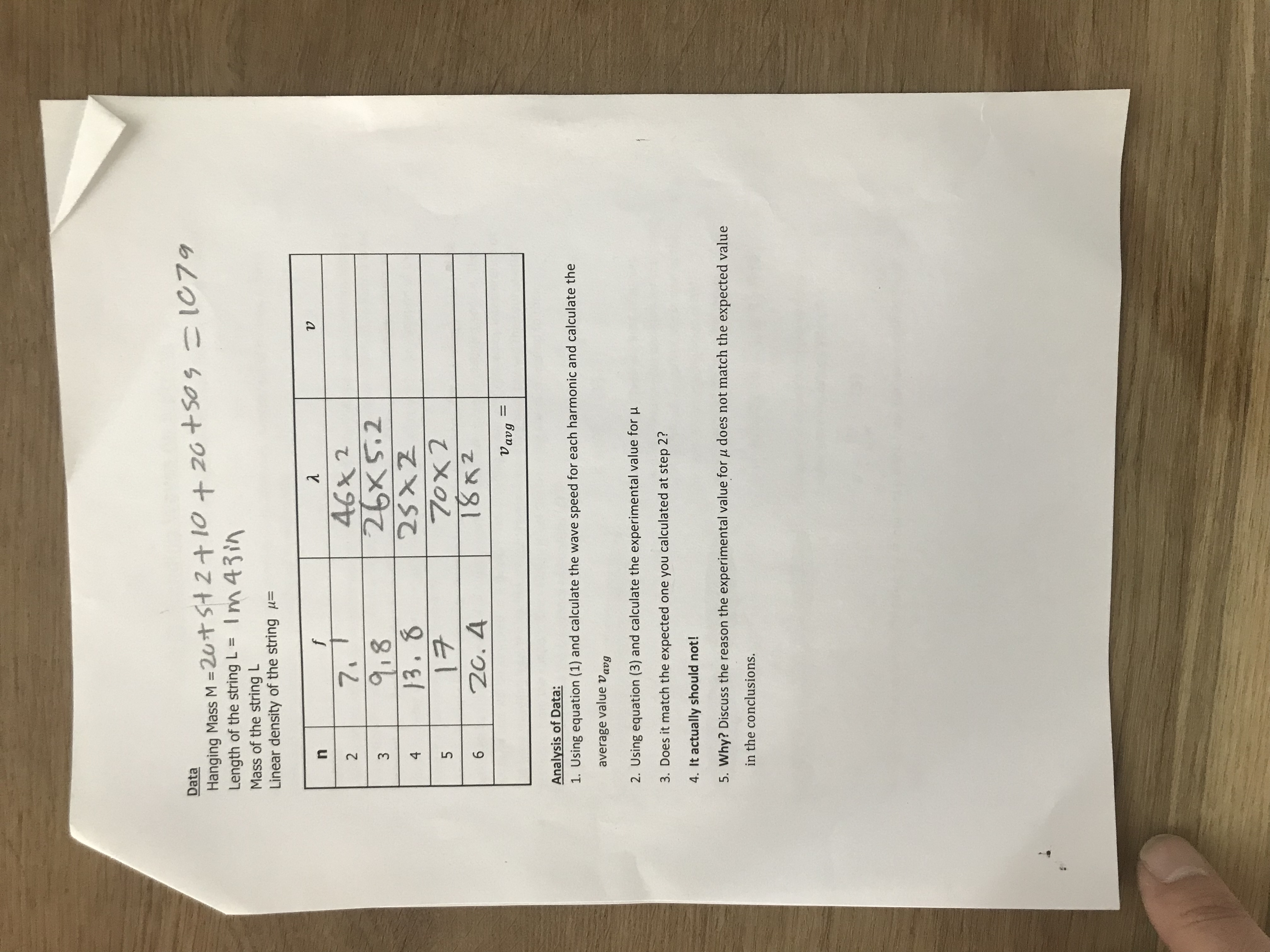
Lab 9: Standing Waves on a String Objective: To explore standing waves on a string and measure the linear density of a stretched elastic string. Apparatus: Vibrator, elastic string, computer interface, mass hanger, set of masses, A-base, pulley and clamp, banana cables and a 2-m meterstick Theory: When two waves of the same frequency and amplitude travel in opposite directions along a string, standing waves are produced. That is, the two traveling waves interfere to form a wave that does not travel along the string. The resulting motion of the string produces points at which the string does not vibrate at all (the nodes) and points at which the vibration of the string is a maximum (the antinodes). In this experiment you will observe standing waves on a string. The standing waves will be produced by vibrating one end of a string with an electrically driven oscillating source. The opposite end will be attached to a support. The standing wave is produced by interference of the wave traveling from the oscillator with the wave traveling back toward the source after reflection from the support. The velocity (v) of the traveling waves is related to their wavelength (2) and the frequency of vibration (f) by: v = af (1) The standing waves are best observed NIX when the resonance condition for the string Node is met. This occurs when the length of the string is an integral number of half wavelengths of the traveling waves. Antinodes L = n(2/2) (n = 1, 2, 3,..) (2) L = 1 A general equation for the velocity of a wave traveling along a string is v = ( 3 ) where Fr is the tension in the string Fr = mg and u is the mass per unit length of the string (M/L).Data Hanging Mass M = 20 + 5+ 2+ 10 + 20+509 = 1079 Length of the string L = 1 m 43in Mass of the string L Linear density of the string = n a v 2 46 x 2 3 918 26x 5.2 4 13. 8 25 x 2 5 17 70x 2 6 20. 4 18 x2 Vavg = Analysis of Data: 1. Using equation (1) and calculate the wave speed for each harmonic and calculate the average value avg 2. Using equation (3) and calculate the experimental value for 3. Does it match the expected one you calculated at step 2? 4. It actually should not! 5. Why? Discuss the reason the experimental value for u does not match the expected value in the conclusions.Procedure: 1) Measure the mass and the length of the string. 2) Calculate the linear density u and record it below. 3) Take the string and run it through the hole on top of the pylon sticking up from the vibrator and tie it to the vertical stand support. 4) Slide the vibrator as close to the tied end as you can get it. 5) Tie a weight to the other end of the cord, and suspend the weight from the pulley. 6) Measure L the distance from the vibrator to the top of the pulley. 7) Hook the vibrator to computer interface and the interface to the pc. 8) Open the Pasco Capstone software, click on the function generator button (on the left of the screen) PASCO capstone" 9) Set the frequency to 25 Hz and Amplitude to 4. 10) Explore the different buttons and learn how to change the frequency. 11) Change the frequency until you produce a second harmonic standing wave. 12) Record the frequency in the table below 13) Measure the distance between two nodes. This represents half of the wavelength. 14) Record the wavelength in the table below. 15) Repeat for harmonics 3, 4, 5 & 6 16) Calculate the wave speed and from that the experimental linear density. string pulley