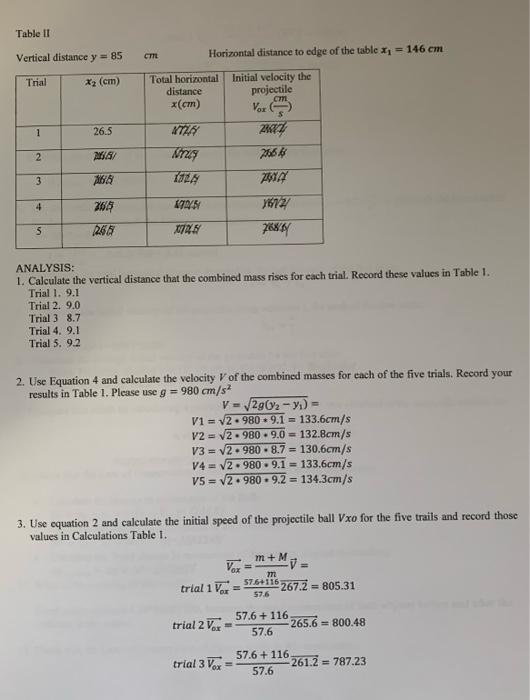
Lab "The Ballistic Pendulum." The Ballistic pendulum experiment combines two conservation laws; conservation of linear momenturn and conservation of energy. If two objects collide and the only force present during the collision is the interaction between them; we could say that the total momentum of the system is conserved. Knowing that linear momentum is defined as mass in motion and calculated as: p= m-V. Then, we could write the Law as: Pi+P)before = (P + P)after For the case of the ballistic pendulum object 1 is the ball and object 2 the cage of the pendulum. Since the pendulum is not moving before the collision then its initial momentum is zero. After collision the ball and the cage travel together, they have the same velocity. Then, we could write: mV (m + M) equation 1 where: m is the mass of the ball: M is the mass of the Pendulum; Varis the initial velcoity of the ball and V is the velocity after ball-pendulum after collision equation 2 Solving for the initial velocity of the ball: Vox=+ The Conservation of Energy states that the total mechanical energy of a system states constant. Which means that if the Kinetic energy of the system decreases the potential energy increases by the same amount. We could write: TE TE or AKE = -AGPE Since in this case the mechanical energy is comprised of Kinetic and Gravitational potential energies and knowing that: KE = mv and GPE = mgy In our case, the pendulum stops at the final position yz Then we find that: (m + M)V = (m+ M)g(y - y) equation 3 From this we find that the velocity of the ball-pendulum system V = 2g(2-) equation 4 m Before Collision M 5 y After Collision Ballistic Pendulum of mass M before and after collision with ball of mass m. PROCEDURES: Part I Ballistic Pendulum 1. se a scale to measure the mass of the ball: m = 57.6 g. 2. Slide the projectile ball (which has a hole in it) onto the rod of the spring gun. 2. When the ball has been placed on the rod, cock the gun by pushing against the ball until the latch catches. Be very careful not to get your hand caught in the spring gun mechanism!!! 3. Fire the gun several times to see how it operates. Ensure the ball lands in the pendulum arm. If you cannot get the arm to catch properly, ask for help. There are several common problems: . The height of the pendulum arm may be off. The opening of the pendulum arm may be at an angle The pendulum arm opening may be lose (which will rotate when the ball hits it, instead of catching it). The pivots at the top of the pendulum arm may be too tight or too lose. 4. A sharp curved point on the side of the pendulum (or on some models a dot) marks the center of mass of the pendulum-ball system. Let the pendulum bob hang vertically and measure the distance y, of the point marking the center of mass above the base of the gun. Record the value of y = 78cm WARNING Ensure the trajectory is clear before cocking the spring and while firing. Safety glasses are available upon request 5. Place the ball on the rod, push against the call to cock the gun, and fire the ball into the stationary pendulum while it hangs freely at rest. The pendulum will catch the ball, swing up, and then lodge in the notched track. 6. Record the vertical distance from the bottom of the base to the center of mass of the ball-pendulum system in Data Table 1. 7. Repeat step 6 four more times for a total of five measurements. 8. Loosen the screws holding the pendulum in its support and remove the pendulum. Use a scale and measure the mass of the pendulum: M = 116g. Data Table 1: Record distances in cm and masses in grams. Trial 1 2 3 Yz (cm) 15.9 15.8 15.5 -1 (cm) 9.1 9.0 8.7 V (cm/s) 133.6 132.8 130.6 Vxo (cm/s) 267.2 265.6 261.2 4 5 15.9 16.0 9.1 9.2 133.6 134.3 267.2 X 1. Position the ballistic pendulum at the edge of the table. 2. Load the ballistic pendulum 268,6 Part II Projectile Motion: In this part, you will determine the initial velocity of ball, projectile by measuring the vertical and horizontal distance traveled. 3. Use a meter stick and measure the distance from the bottom of the ball to the floor, this is your vertical distance y. This measurement will be used to calculate the time of fall of the projectile. 4. Fire the ball and pay attention to where the ball first contacts the floor, place a carboard there or a white sheet of paper. This will help you determine the exact position where the ball lands. 5. Measure the horizontal distance from where the ball is released to the edge of the table, let's called this distance x. 6. Load the ballistic pendulum and fire the ball, find the marking left by the ball on the place that it landed. 7. Measure the horizontal distance between the edge of the table and the place where the ball landed, this is distance x- 8. Record these measurements in Table II. 9. Repeat 7 and 8 four more times for a total of five measurements. Table II Vertical distance y = 85 Trial X (cm) 1 2 3 4 5 26.5 2016/5/ 76 26.5 (2.56 5 cm Total horizontal Initial velocity the projectile cm Vox distance x(cm) Nrzy TOLA Horizontal distance to edge of the table x = 146 cm 110/51 TITLE ANALYSIS: 1. Calculate the vertical distance that the combined mass rises for each trial. Record these values in Table 1. Trial 1. 9.11 Trial 2.9.0 Trial 3 8.7 Trial 4. 9.1 Trial 5. 9.2 2. Use Equation 4 and calculate the velocity of the combined masses for each of the five trials. Record your results in Table 1. Please use g = 980 cm/s 133.6cm/s V = 2g(y-y) = V1= 2 980 9.1 = V2 = 2 980 9.0 = 132.8cm/s V3= 2 980 8.7= 130.6cm/s V4 = 2.980.9.1 = 133.6cm/s V5 = 2 980 9.2 = 134.3cm/s 3. Use equation 2 and calculate the initial speed of the projectile ball Vxo for the five trails and record those values in Calculations Table 1. trial 1 Vor 2014 776643 7361 Vox trial 2 Vox= trial 3 Vox 16/12/ 768/8/ = m+M m 57.6+116: 57.6 = V= 267.2=805.31 57.6+116. 57.6 265.6 800.48 57.6+ 116. 57.6 261.2 = 787.23 trial 4 V H trial 5 V 57.6+116. 57.6 167.2 - 503.92 $76+116 268.6 809.53 STA 4. Calculate the average of the initial velocity of the ball from the five trials: (Vox)ave=245.96cm/s 5. Use the vertical distance, the value for the gravitational acceleration g = 980, to calculate the time it takes for the projectile to reach the floor: Vertical distance Y=78+7=85 cm 2x8.5/980 = 0.42 second 6. Determine the total horizontal distance traveled by the ball for each of the five trials: x = x + x 7. Determine the initial velocity of the projectile using equation 1, for each of the five trials: (172.5*3)*5-258.75cm/s 8. Calculate the average initial velocity of the projectile for the five trials Using Projectile Moto 19 17.04.2-481228-8 9. Compare this result by calculating a percentage difference with the one obtained in the projectile motion lab: Ivalue 1-value 21 x 100% (value1 + value 2) % difference =- 78% 10. Check that the Law of Conservation of Momentum is held in this experiment: Calculate the change in momentum of the Ball: Ap=Pr-Pi = m(V-Vox)-124435 . Calculate the change in momentum of the Pendulum: AP= P-P = M(V-0)-A6425.68 Calculate the Total change in momentum of the system, explain its meaning: APsystem Ap+AP-226707 11. What is the meaning of this result? Total momentum is CONSERVED, because the total momentum of both objects before and after the collision is the same. 12. Check that the Law of Conservation of Energy holds in this experiment: Calculate The total energy of the Ball-Pendulum system right after collision; TE = KEball-pendulum =(m + M)V-53x Calculate The total energy of the Ball-Pendulum system at the highest vertical position; TE GPE (M+m)g(y2-ys)ave MAS . 13. What is the meaning of this result? Total mechanical energy is CONSERVED, because the energy can neither be created nor be destroyed; it can only be internally converted from one form to another if the forces doing work on the system are conservative in nature. 14. What are the different types of collisions, how do you classify them? What collision is taking place in this lab, how do you know? Collisions are two types Elastic Collision = An elastic collision occurs when the two objects "bounce" apart when they collide Inclastic Collision - An inelastic collision occurs when two objects collide and do not bounce away from each other. This is inelastic collision because the two-particle stich to gather after collision. CONCLUSIONS: I. Definitions: Linear Momentum - the momentum of translation being a vector quantity in classical physics equal to the product of the mass and the velocity of the center of mass. Impulse- term that quantifies the overall effect of a force acting over time. It is conventionally given the symbol J, end text and expressed in Newton-seconds. Statement for the Momentum-Impulse Theorem - states that the change in momentum of an object equals the impulse applied to it. Statement for Conservation of Linear Momentum - expresses the fact that a body or system of bodies in motion retains its total momentum, the product of mass and vector velocity, unless an external force is applied to it. Kinetic Energy - energy which a body possesses by virtue of being in motion. . Potential Energy - the energy possessed by a body by virtue of its position relative to others, stresses within itself, electric charge, and other factors. Statement for the Law of Conservation of Energy - the energy possessed by a body by virtue of its position relative to others, stresses within itself, electric charge, and other factors. II. Equations: For all the Physical quantities and Laws used and the derivation of the conservation of momentum. Linear Momentum-P-mv Impulse-Ap = FAt Momentum-Impulse Theorem - J - Ap o If mass is constant, then - FA-mav o If mass is changing, then - F dtm dv + v dm