Language: C

The partially completed progra (please finish this using the instructions above):

/*---------------------------------------------------- File: incremSearchFncSoln.c Name: XXX Student ID: XXX This program plots function, asks the user to select an interval for finding roots. Function: f(x) = 50 - x^2 |cos(x^1/2)| An incremental search root finding method is used. ------------------------------------------------------*/ #include #include #include "gng1106plplot.h" #define N 100 // number of points #define MAX_ROOTS 3 // Maximum number of roots #define TRUE 1 #define FALSE 0 #define ALMOST_0 1e-5 // For testing zero values #define SI_RESOLUTION 1000 // Subinterval resolution // Function Prototypes void findInterval(double *, double *); int findAllRoots(double, double, double []); int findRoot(double, double, double *); void plotFunc(double, double, int, double []); double func(double); void plot(int, double[], double[], int, double[], double[]); double getMin(double *, int ); double getMax(double *, int ); /*-------------------------------------------------------- Function: main() Description: Call findInterval to allow the user to select an interval for searching. Show the results to the user. ---------------------------------------------------------*/ int main() { double start, end; double roots[MAX_ROOTS]; int n; // number of roots found int ix; // Get intervals from user findInterval(&start, &end); printf("Finding roots for intervals between %.4f and %.4f ", start, end); n = findAllRoots(start, end, roots); printf("Found %d roots: ",n); for(ix = 0; ix

f(x) = 50 - x^2 |cos(sqrt(x)| , x must be positive, if x negative return 0. -----------------------------------------------------------*/ double func(double x) { /* Complete this function */ } /*---------------------------------------------------------- Function: plotFunc Parameters: begin, end: beginning and end of interval (x values) to plot nRoots - number of roots in the root array. root - value of root when flag is TRUE. Description: Plot the function on the interval between begin and end. Plots an x at the roots if nRoots > 0. ---------------------------------------------------------------*/ void plotFunc(double begin, double end, int nRoots, double roots[]) { double x[N]; double y[N]; double inc; // increment for incrementing x double yRoots[nRoots]; int ix; // Calculate function points inc = (end - begin)/N; x[0] = begin; y[0] = func(x[0]); // Compute first point for(ix = 1; ix

/*------------------------------------------------- Function: plot() Parameters: n: number of points in the arrays xPtr: pointer to x values (horizontal axis). yPtr: pointer to y values (vertical axis). rRoots: number of roots xRoots: x coordinate of roots yRoots: y coordinate of roots. Return value: none. Description: Initialises the plot. The following values in the referenced structure are used to setup the plot: x[0], x[n-1] - assume that x values are sequential miny, maxy - vertical axis range (add 10% to min/max value) Sets up white background and black forground colors. Then plots the curve accessed using xPtr and yPtr. Plots x at the root points. -------------------------------------------------*/ void plot(int n, double *xPtr, double *yPtr, int nRoots, double *xRoots, double *yRoots) { double miny, maxy; double range; // range of vertical axix // Setup plot configuration plsdev("wingcc"); // Sets device to wingcc - CodeBlocks compiler // Initialise the plot plinit(); // Configure the axis and labels plwidth(3); // select the width of the pen // Find range for axis miny = getMin(yPtr, n); maxy = getMax(yPtr, n); range = maxy - miny; // the width of the range maxy = maxy + 0.1*range; miny = miny - 0.1*range; plenv0(xPtr[0], xPtr[n-1], miny, maxy, 0, 1); plcol0(GREEN); // Select color for labels pllab("x", "f(x)", "Function"); // Plot the velocity. plcol0(BLUE); // Color for plotting curve plline(n, xPtr, yPtr); // Plot the points if(nRoots > 0) { plcol0(RED); plpoin(nRoots,xRoots, yRoots, 'x'); } plend(); } /*---------------------------------------------------------- Function: getMin Parameters: array - reference to an array with double values n - number of elements in the array Returns min: the minimum value found in the array Description: Traverses the array to find its minimum value. ----------------------------------------------------------------*/ double getMin(double *array, int n) { int ix; double min = array[0]; for(ix = 1; ix array[ix]) min = array[ix]; return(min); }

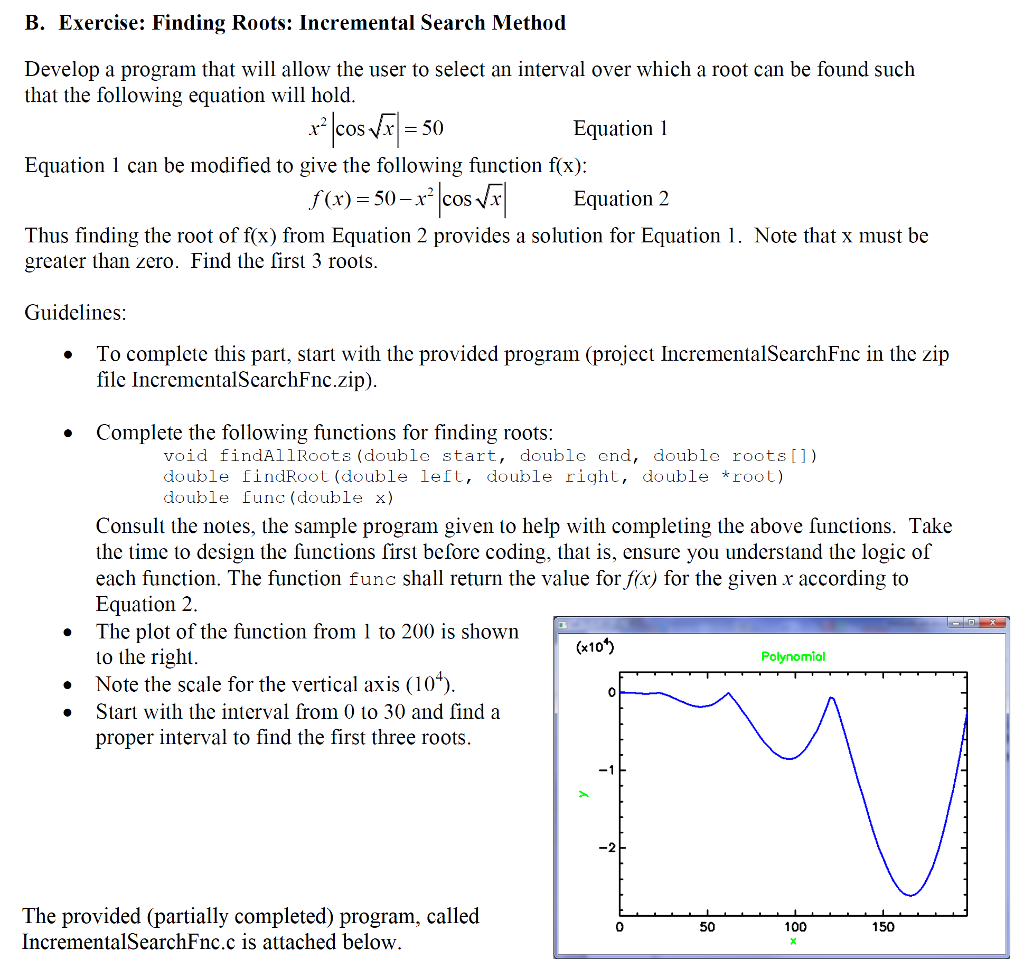
/*---------------------------------------------------------- Function: getMax Parameters: array - reference to an array with double values n - number of elements in the array Returns max: the maximum value found in the array Description: Traverses the array to find its maximum value. ----------------------------------------------------------------*/ double getMax(double *array, int n) { int ix; double max = array[0]; for(ix = 1; ix B. Exercise: Finding Roots: Incremental Search Method Develop a program that will allow the user to select an interval over which a root can be found such that the following equation will hold Equation 1 can be modified to give the following function f(x) Thus finding the root of f(x) from Equation 2 provides a solution for Equation 1. Note that x must be Equation1 f(x) = 50-x2lcos.g Equation 2 greater than zero. Find the first 3 roots Guidelines To complete this part, start with the provided program (projcct IncrementalSearchFnc in the zip file IncrementalScarchFnc.zip) Complete the following functions for finding roots: void findAllRoots (double start, double cnd, double roots[]) double indRoot (double left, double right, double *root) double func (double x) Consult the notes, the sample program given to help with completing the above functions. Take the time to design the functions first before coding, that is, ensure you understand the logic of each function. The function func shall return the value for fx) for the given r according to Equation 2. The plot of the function from 1 to 200 is shown to the right (x10 Polynomiol . Note the scale for the vertical axis (10*) Start with the interval from 0 to 30 and find a proper interval to find the first three roots 2 The provided (partially completed) program, called IncrementalSearchFnc.c is attached below. 0 50 100 150 B. Exercise: Finding Roots: Incremental Search Method Develop a program that will allow the user to select an interval over which a root can be found such that the following equation will hold Equation 1 can be modified to give the following function f(x) Thus finding the root of f(x) from Equation 2 provides a solution for Equation 1. Note that x must be Equation1 f(x) = 50-x2lcos.g Equation 2 greater than zero. Find the first 3 roots Guidelines To complete this part, start with the provided program (projcct IncrementalSearchFnc in the zip file IncrementalScarchFnc.zip) Complete the following functions for finding roots: void findAllRoots (double start, double cnd, double roots[]) double indRoot (double left, double right, double *root) double func (double x) Consult the notes, the sample program given to help with completing the above functions. Take the time to design the functions first before coding, that is, ensure you understand the logic of each function. The function func shall return the value for fx) for the given r according to Equation 2. The plot of the function from 1 to 200 is shown to the right (x10 Polynomiol . Note the scale for the vertical axis (10*) Start with the interval from 0 to 30 and find a proper interval to find the first three roots 2 The provided (partially completed) program, called IncrementalSearchFnc.c is attached below. 0 50 100 150