Question: Language, Proof, and Logic exercise 10.10 and 10.12 help? 470 (290 of 100% Du Each of the following arguments is valid. Some of the conclusions

Language, Proof, and Logic exercise 10.10 and 10.12 help?

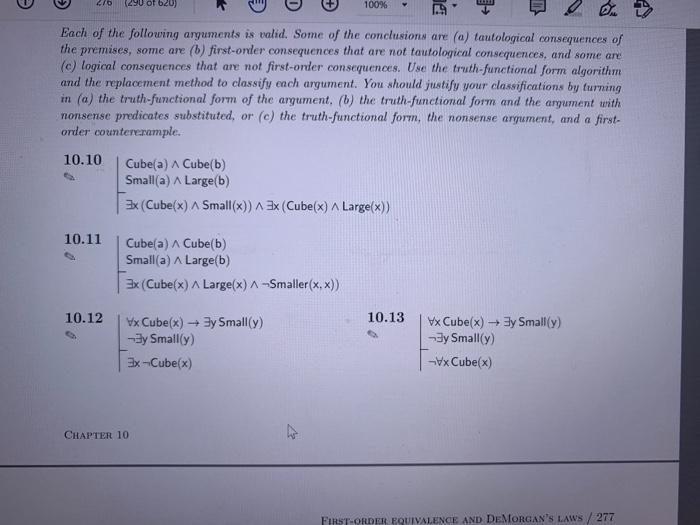
470 (290 of 100% Du Each of the following arguments is valid. Some of the conclusions are (a) tautological consequences of the premises, some are (b) first-order consequences that are not tautological consequences, and some are (c) logical consequences that are not first-order consequences. Use the truth-functional form algorithm and the replacement method to classify each argument. You should justify your classifications by turning in (a) the truth-functional form of the argument. (b) the truth-functional form and the argument with nonsense predicates substituted, or (c) the truth-functional form, the nonsense argument, and a first- order counterexample. 10.10 Cube(a) Cube(b) Small(a) A Large(b) x (Cube(x) A Small(x)) A 3x (Cube(x) A Large(x)) 10.11 Cube(a) Cubelb) Small(a) A Large(b) 3x (Cube(x) A Large(x) A-Smaller(x,x)) 10.12 10.13 Vx Cube(x) + 3y Small(y) By Small(y) Ex-Cube(x) Vx Cube(x) + 3y Small(y) By Small(y) -VxCube(x) CHAPTER 10 FIRST-ORDER EQUIVALENCE AND DEMORGAN'S LAWS / 277 470 (290 of 100% Du Each of the following arguments is valid. Some of the conclusions are (a) tautological consequences of the premises, some are (b) first-order consequences that are not tautological consequences, and some are (c) logical consequences that are not first-order consequences. Use the truth-functional form algorithm and the replacement method to classify each argument. You should justify your classifications by turning in (a) the truth-functional form of the argument. (b) the truth-functional form and the argument with nonsense predicates substituted, or (c) the truth-functional form, the nonsense argument, and a first- order counterexample. 10.10 Cube(a) Cube(b) Small(a) A Large(b) x (Cube(x) A Small(x)) A 3x (Cube(x) A Large(x)) 10.11 Cube(a) Cubelb) Small(a) A Large(b) 3x (Cube(x) A Large(x) A-Smaller(x,x)) 10.12 10.13 Vx Cube(x) + 3y Small(y) By Small(y) Ex-Cube(x) Vx Cube(x) + 3y Small(y) By Small(y) -VxCube(x) CHAPTER 10 FIRST-ORDER EQUIVALENCE AND DEMORGAN'S LAWS / 277

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

Hi there, I have a presentation needed to be done next week. Company Law course. there is an article to read and summarize so I can present in 4 to 5 minutes. Could anyone help me to do this before...

Assignment 1 Instructions and Guidelines Word Limit 1000 words Write400-500wordsforeachquestion Disclosethewordcountinyourfinalsubmission...

Please answer: a discussion of the ethical issues involved. The court might not itself consider the ethics of the actions of the parties. However, I ask that you consider the ethics of the following:...

1) a brief recitation of the facts of the case, indicating the identities of the parties, their relationship 2) a brief recitation of the issue(s) considered by the court as it analyzes the...

Please answer a summary of the court's decision on the issue and the reason why the court came to this decision I. BACKGROUND This case originated in the Circuit Court in and for Broward County,...

CLOSING ARGUMENTS A Closing Argument should: 1. Repeat your theory and theme of the case 2. Summarize the evidence that preceded it 3. Relate the evidence to the law and the legal issues (i.e....

Sidhu v. Canada (Citizenship and Immigration), 2012 FC 515 (CanLII) [1] This is an application undersubsection 72(1) of the Immigration and Refugee Protection Act , SC 2001, c. 27 (Act) for judicial...

Opening Statement for Defense The 1948 U.S. Presidential election was a hard fight for Harry Truman. No one thought he had a shot and the folks at the Chicago Daily Tribune didn't think so either. At...

Refer to the list of stakeholders and their objectives in Exhibit 1.1. For each stakeholder group, state at least one additional concern that you think might shape how organizations manage human...

What is the net present value of the following project? The discount rate is 12%. The initial investment is $16 and the project has a 5-year duration. YEAR CASH INFLOWS 1 1,000 2 4,000 3 3,000 4...

On January 1 , 2 0 2 5 , Haberstad, Inc., learns that a competitor s process to develop a product that would compete fiercely with Haberstad, Inc., s has progressed significantly. Based on this, the...

Discuss several ways ( at least four ways ) to improve the requirement process and thus, a project team can avoid a situation where too many changes to the project requirements occur at the later...

=+ How can they be incorporated into social media content?

=+Generation Z. Then, propose one strategy and two tactics you could implement to reach this audience for Samsung. Discuss how you would evaluate the effectiveness of this campaign.

=+3. Identify the different writing styles discussed in the chapter. Which ones do you feel are the most effective for brands? Which ones best describe how you approach social media?