Larry, Moe and Curly work in a clock factory. Larry and Moe can each work 40 hours per week and Curly can work 20 hours per week. The company makes two types of clocks: grandfather clocks and wall clocks. Each grandfather clock sold results in a profit of $300 and each wall clock sold results in a profit of $200. Larry assembles the clock mechanism, while Moe carves the wood casing. Curly takes orders and ships the clocks. The time for these operations is shown in the table below.

Operation	Time Required
	Grandfather clock	Wall clock
assembly	6 hours	3 hours
carving	8 hours	5 hours
shipping	2 hours	2 hours

Max profit: 300x_g + 200x_w

s.t : 6x_g + 3x_w 40 (assembly constraint)

8x_g+ 5x_w 40 (carving constraint)

2x_g + 2x_w 20 ( shipping constraint)

x_g, x_w 0

Suppose I solved this problem using excel and read the following from the sensitivity analysis report

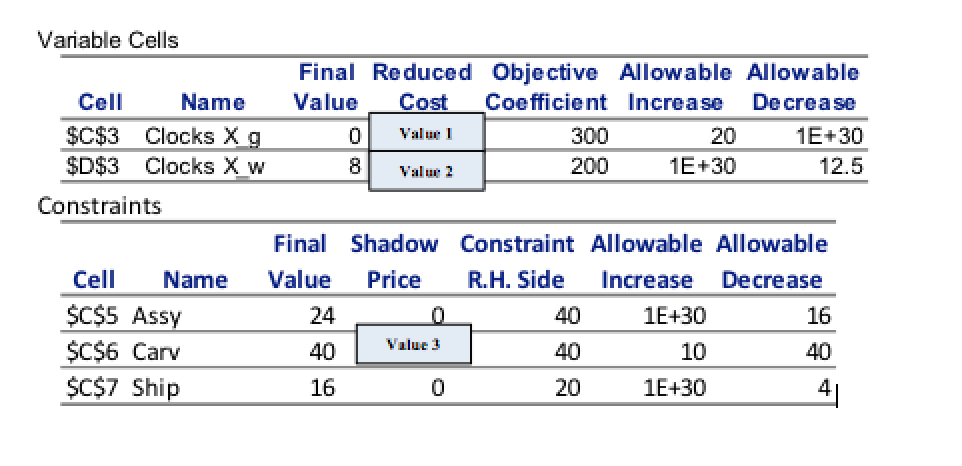
a. What can you say about the missing values 1, 2 and 3 in the reduced cost column and the shadow price? Are they zero or a non-zero value and can you discuss if they are negative or positive? Explain briefly.

Value 1: ----------------------------------------------------------------------------------------------------------

Value 2: ----------------------------------------------------------------------------------------------------------

Value 3: ----------------------------------------------------------------------------------------------------------

b. How much of each clock do I make and what is my optimal profit?

c. By how much can the per unit profit for a grandfather clock change before my current optimal solution would no longer be optimal

d. How much would I be willing to pay Moe (carving) to work 5 additional hours for carving? How about 12 additional hours for carving?

Variable Cells Cell $C$3 $D$3 Name Clocks Xg Clocks Xw Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase De crea se 0 300 20 1E+30 8 Value 2 200 1E+30 12.5 Constraints Cell Name $C$5 Assy $C$6 Carv $C$7 Ship Final Shadow Constraint Allowable Allowable Value Price R.H. Side Increase Decrease 24 0 40 1E+30 16 40 Value 1 40 10 40 16 0 20 1E+30 4 Variable Cells Cell $C$3 $D$3 Name Clocks Xg Clocks Xw Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase De crea se 0 300 20 1E+30 8 Value 2 200 1E+30 12.5 Constraints Cell Name $C$5 Assy $C$6 Carv $C$7 Ship Final Shadow Constraint Allowable Allowable Value Price R.H. Side Increase Decrease 24 0 40 1E+30 16 40 Value 1 40 10 40 16 0 20 1E+30 4