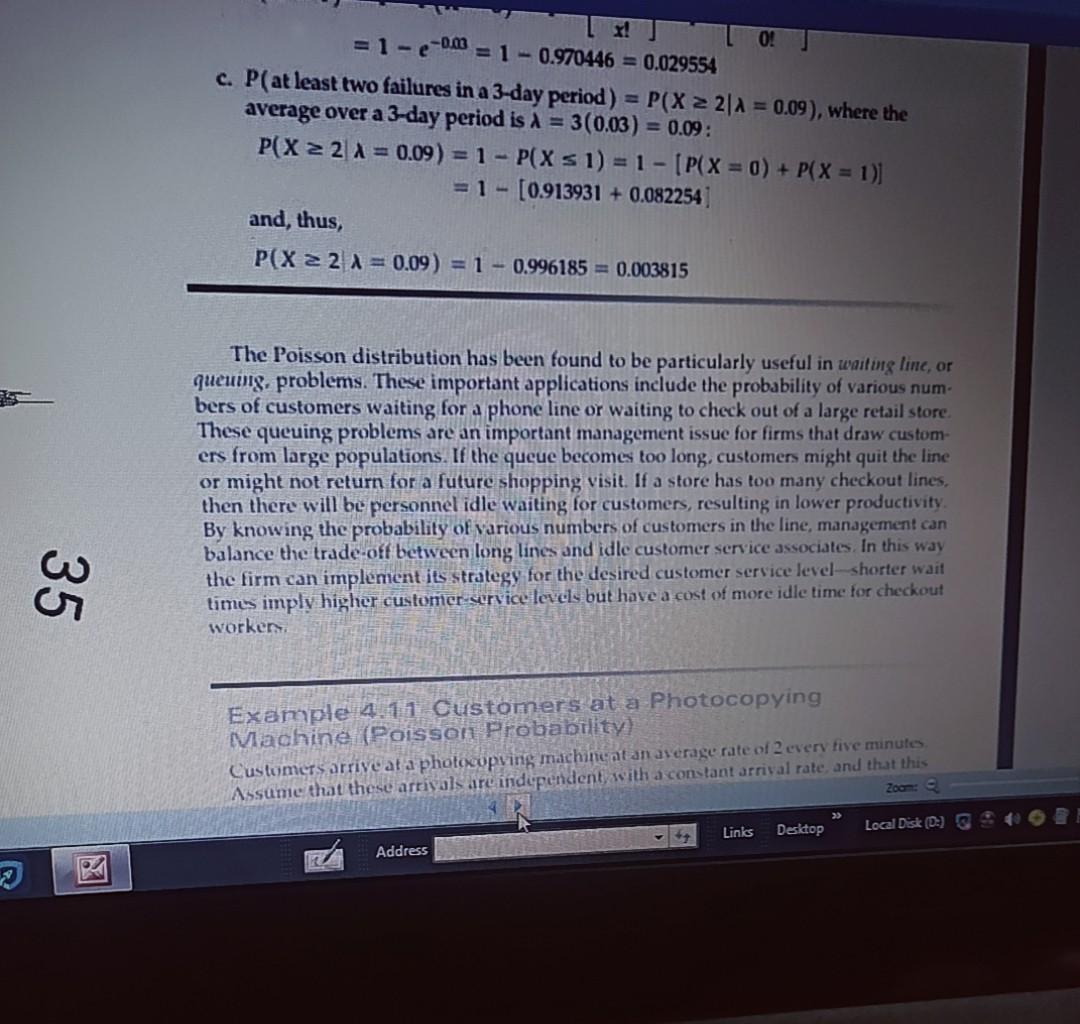
= l-e-00 X! 0! = 1 -0.970446 = 0.029554 c. P(at least two failures in a 3-day period) = P(X 22/4 = 0.09), where the average over a 3-day period is a = 3(0.03) = 0.09 : P(X 2 2 4 = 0.09) = 1 - P(X s 1) = 1 - [P(X = 0) + P(X = 1)] 1- - (0.913931 + 0.082254] and, thus, P(X 22 X = 0.09) = 1 - 0.996185 = 0.003815 The Poisson distribution has been found to be particularly useful in waiting line, or queunig, problems. These important applications include the probability of various num- bers of customers waiting for a phone line or waiting to check out of a large retail store. These queuing problems are an important management issue for firms that draw custom- ers from large populations. If the queue becomes too long, customers might quit the line or might not return for a future shopping visit. If a store has too many checkout lines, then there will be personnel idle waiting for customers, resulting in lower productivity By knowing the probability of various numbers of customers in the line, management can balance the trade-off between long lines and idle customer service associates. In this way the firm can implement ils strategy for the desired customer service level shorter wait times imply higher customer service levels but have a cost of more idle time for checkout workers 35 Example 4.11 Customers at a Photocopying Machine (Poisson Probability) Customers arrive at a photocopving machine at an average rate of every five minutes Assume that these arrivals are indipendent, with a constant arrival rate, and that this 200 Linis Desktop Local Disk (D) $ Address = l-e-00 X! 0! = 1 -0.970446 = 0.029554 c. P(at least two failures in a 3-day period) = P(X 22/4 = 0.09), where the average over a 3-day period is a = 3(0.03) = 0.09 : P(X 2 2 4 = 0.09) = 1 - P(X s 1) = 1 - [P(X = 0) + P(X = 1)] 1- - (0.913931 + 0.082254] and, thus, P(X 22 X = 0.09) = 1 - 0.996185 = 0.003815 The Poisson distribution has been found to be particularly useful in waiting line, or queunig, problems. These important applications include the probability of various num- bers of customers waiting for a phone line or waiting to check out of a large retail store. These queuing problems are an important management issue for firms that draw custom- ers from large populations. If the queue becomes too long, customers might quit the line or might not return for a future shopping visit. If a store has too many checkout lines, then there will be personnel idle waiting for customers, resulting in lower productivity By knowing the probability of various numbers of customers in the line, management can balance the trade-off between long lines and idle customer service associates. In this way the firm can implement ils strategy for the desired customer service level shorter wait times imply higher customer service levels but have a cost of more idle time for checkout workers 35 Example 4.11 Customers at a Photocopying Machine (Poisson Probability) Customers arrive at a photocopving machine at an average rate of every five minutes Assume that these arrivals are indipendent, with a constant arrival rate, and that this 200 Linis Desktop Local Disk (D) $ Address