Learning Goal:

To section a composite shape into simple shapes so the moment$-$ofinertia tables and the parallel$-$axis theorem can be used to find the moment of inertia of the composite shape.

Tables listing moments of inertia cannot contain the formula for every possible shape that can be built. However, many shapes can be sectioned into pieces that have entries in the tables. Consider the shape in the following figure,

$($Figure $1)$

This shape can be sectioned into three rectangles as so$,$

$($Figure $2)$

Because the moment of inertia of a rectangle is a well$-$known formula, the moment of inertia for the full composite can be found by calculating the individual moments of inertia of the three sections and adding them. Because the centroids of the vertical sections do not align with the $\backslash ($ x $\backslash )$ or $\backslash ($ y $\backslash )$ axes, we will need to use the parallel$-$axis theorem to calculate the moments of inertia of those sections. The moment of inertia for a crosssection where the centroid of the cross$-$section does not align with the reference axis is given by

$\backslash [$

I$=\backslash$bar$\{$I$\}+$A d$^\{2\}$

$\backslash ]$

where $\backslash (\backslash$bar$\{$I$\}\backslash )$ is the moment of inertia of the cross$-$section with respect to its centroid, $\backslash ($ A $\backslash )$ is the area of the cross$-$section, and $\backslash ($ d $\backslash )$ is the perpendicular distance from the reference axis to the centroid of the cross$-$section.

Because the principle of superposition applies to moments of inertia, we are free to section a shape in any way we like, provided no part of the shape is left out or contained in more than one section. The original shape could have been sectioned in the following manner,

$($Figure $3)$

and the calculated moment of inertia for the composite would have been the same. Part of the "art" of finding the moment of inertia of a composite shape is determining how to section the shape. For example, if the moment of inertia about the $\backslash ($ y $\backslash )$ axis were needed, the first sectioning would be better. The second sectioning makes calculating the moment of inertia about the $\backslash ($ x $\backslash )$ axis easier.

For this tutorial, you will need the following moments of inertia:

Figure

Correct

Part B $-$ Moment of Inertia of a Composite Beam about the $\backslash ($ y $\backslash )$ axis

For the beam from Part A $($shown again here for reference$),$ calculate the moment of inertia about the $\backslash ($ y $\backslash )$ axis.

$($Figure $7)$

The dimensions are $\backslash ($ d$\_\{1\}=7\mathrm{.}0\backslash$mathrm$\{$in$\},$ d$\_\{2\}=16\mathrm{.}5\backslash$mathrm$\{$in$\},$ d$\_\{3\}=8\mathrm{.}0\backslash$mathrm$\{$in$\}\backslash ),$ and $\backslash ($ t$=0\mathrm{.}80\backslash$mathrm$\{$in$\}\backslash ).$

Express your answer to three significant figures and include the appropriate units.

View Available Hint$($s$)$

Incorrect; Try Again; $3$ attempts remaining

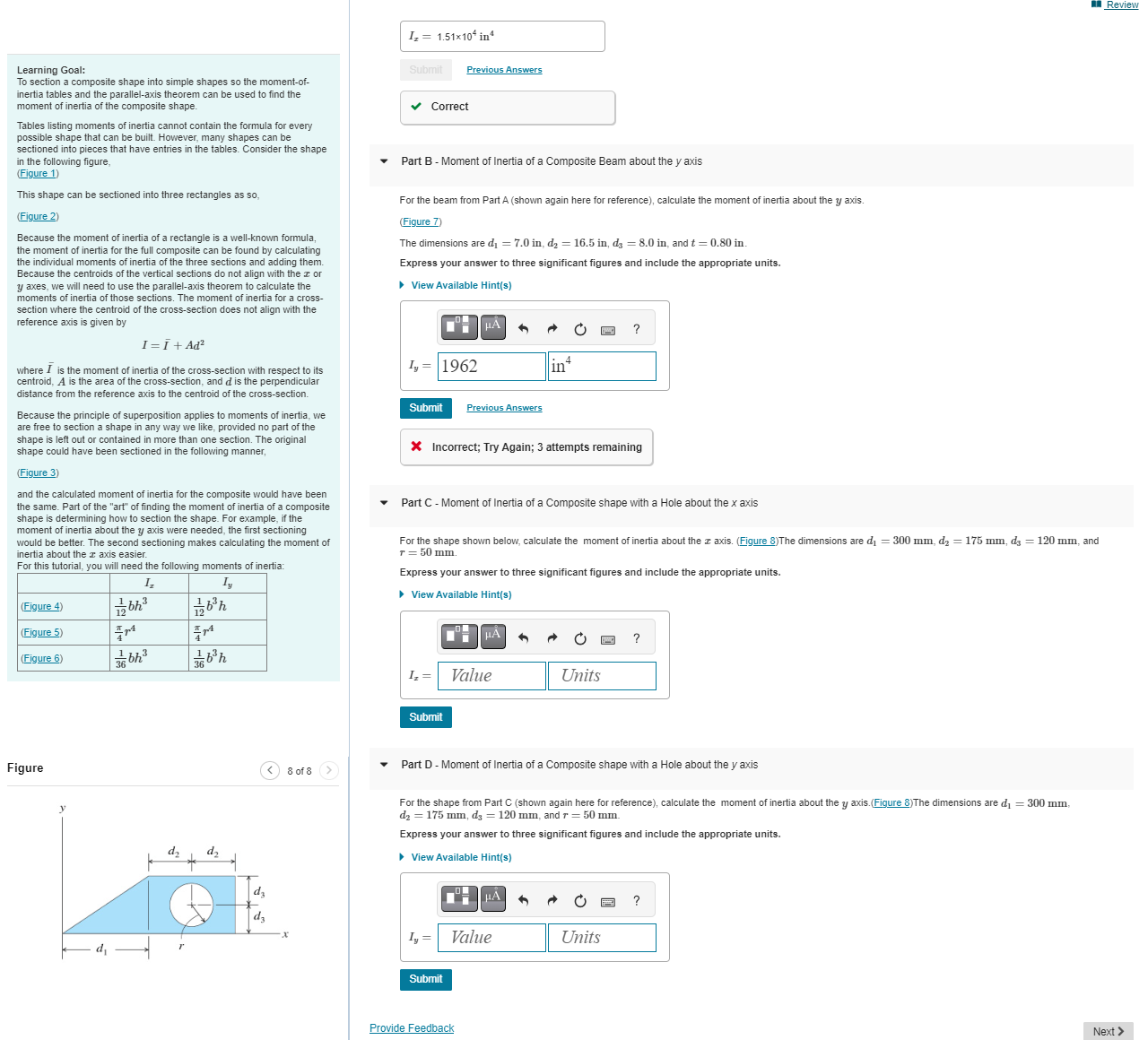
Part C $-$ Moment of Inertia of a Composite shape with a Hole about the $\backslash ($ x $\backslash )$ axis

For the shape shown below, calculate the moment of inertia about the $\backslash ($ x $\backslash )$ axis. $($Figure $8)$ The dimensions are $\backslash ($ d$\_\{1\}=300\backslash$mathrm$\{$~mm$\},$ d$\_\{2\}=175\backslash$mathrm$\{$~mm$\},$ d$\_\{3\}=120\backslash$mathrm$\{$~mm$\}\backslash ),$ and $\backslash ($ r$=50\backslash$mathrm$\{$~mm$\}\backslash ).$

Express your answer to three significant figures and include the appropriate units.

View Available Hint$($s$)$

$\backslash [$

I$\_\{$z$\}=\backslash$square

$\backslash ]$

Part D $-$ Moment of Inertia of a Composite shape with a Hole about the $\backslash ($ y $\backslash )$ axis

For the shape from Part $\backslash ($ C $\backslash )($shown again here for reference$),$ calculate the moment of inertia about the $\backslash ($ y $\backslash )$ axis.$($Figure $8)$ The dimensions are $\backslash ($ d$\_\{1\}=300\backslash$mathrm$\{$~mm$\}\backslash ),\backslash ($ d$\_\{2\}=175\backslash$mathrm$\{$~mm$\},$ d$\_\{3\}=120\backslash$mathrm$\{$~mm$\}\backslash ),$ and $\backslash ($ r$=50\backslash$mathrm$\{$~mm$\}\backslash ).$

Express your answer to three significant figures and include the appropriate units.

View Available Hint$($s$)$

$\backslash [$

I$\_\{$y$\}=\backslash$square

$\backslash ]$