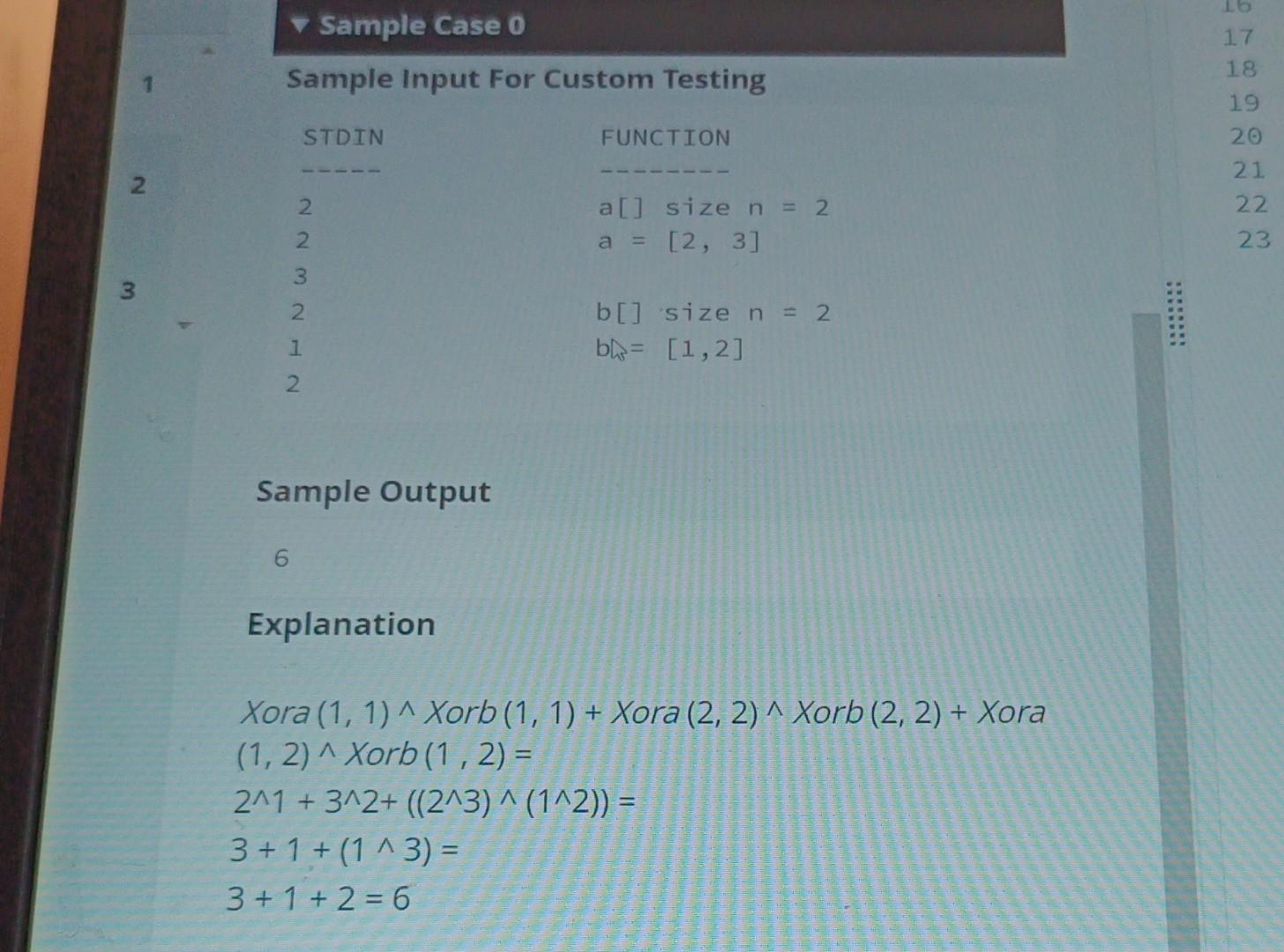
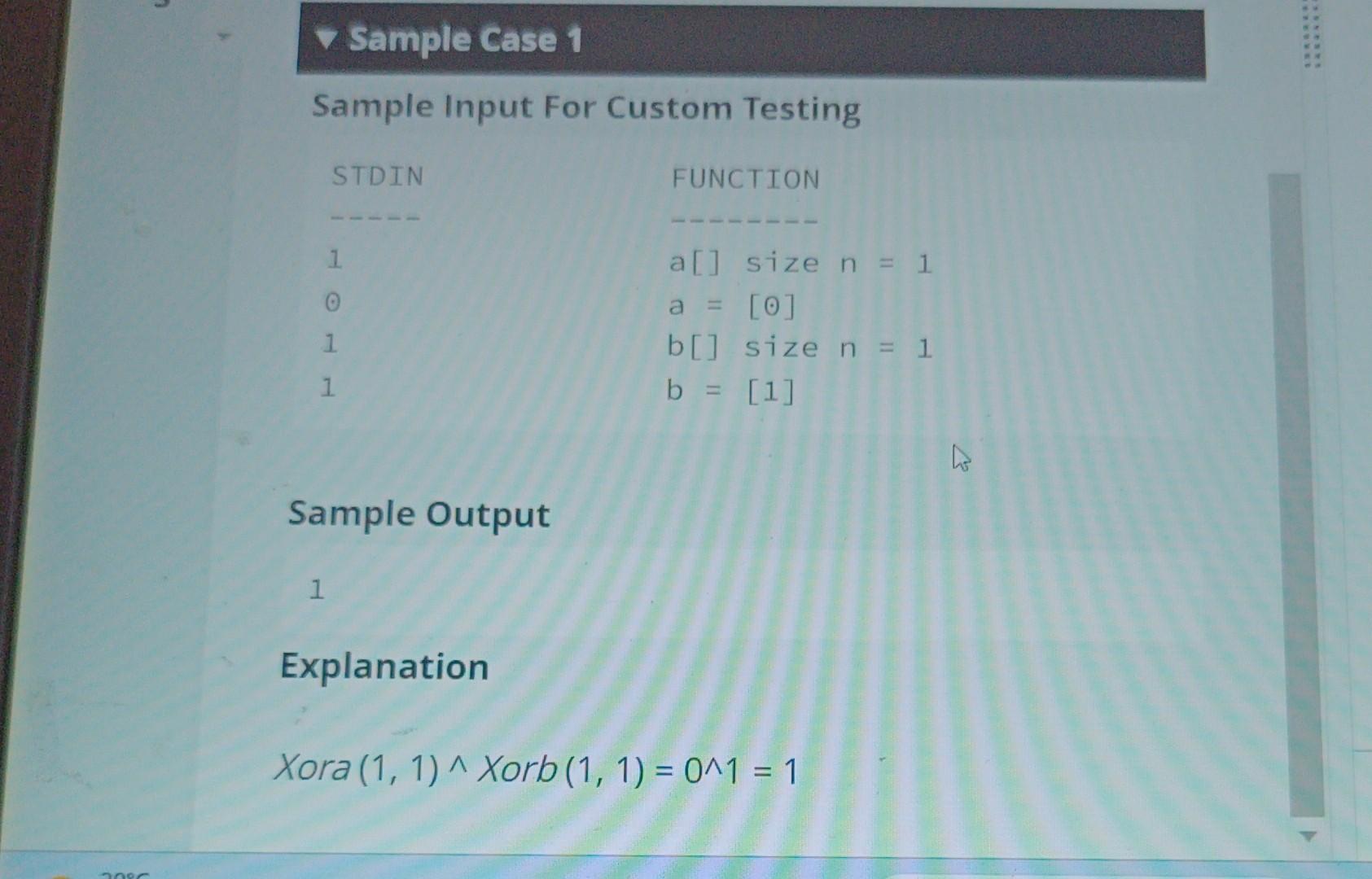
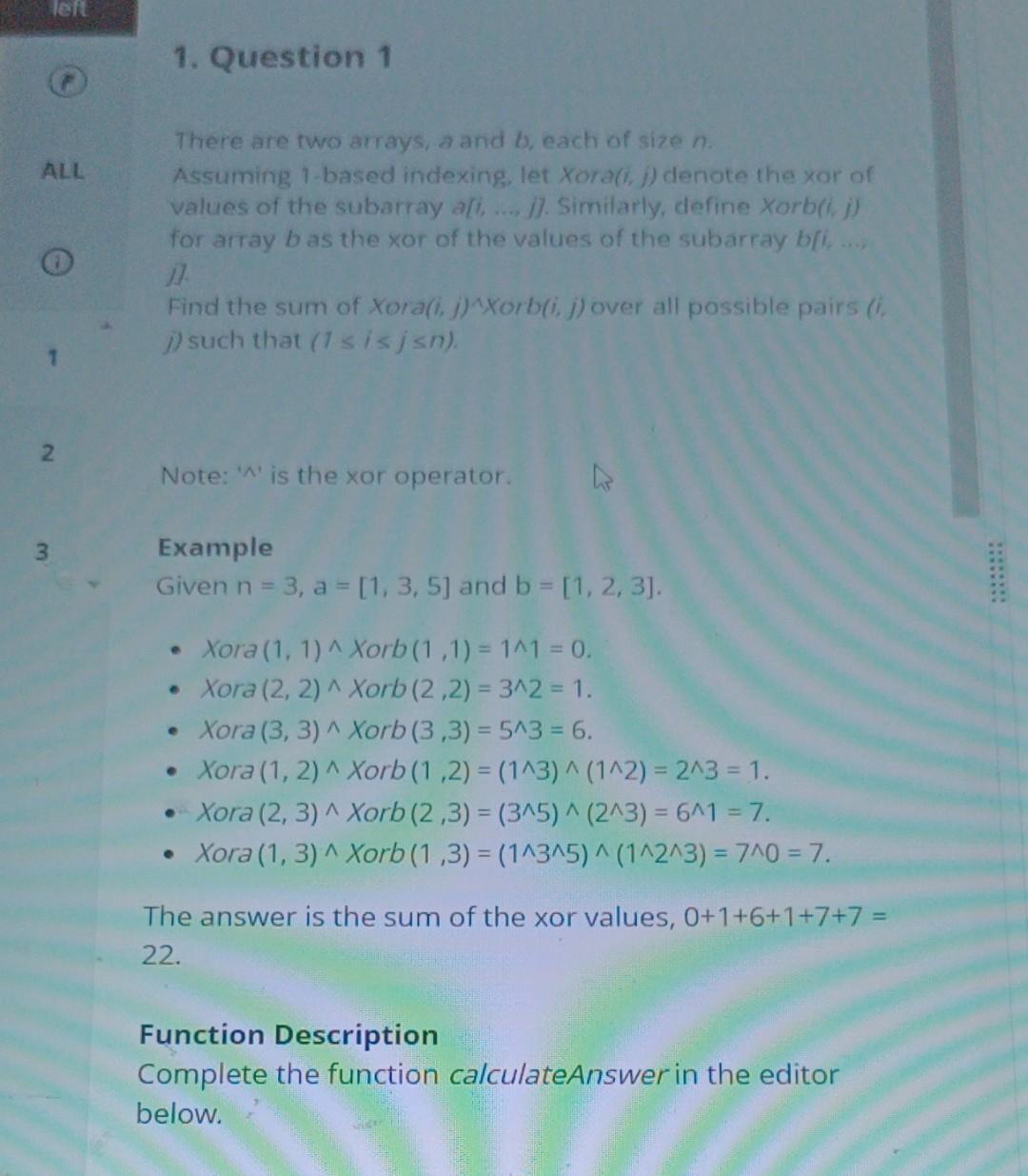
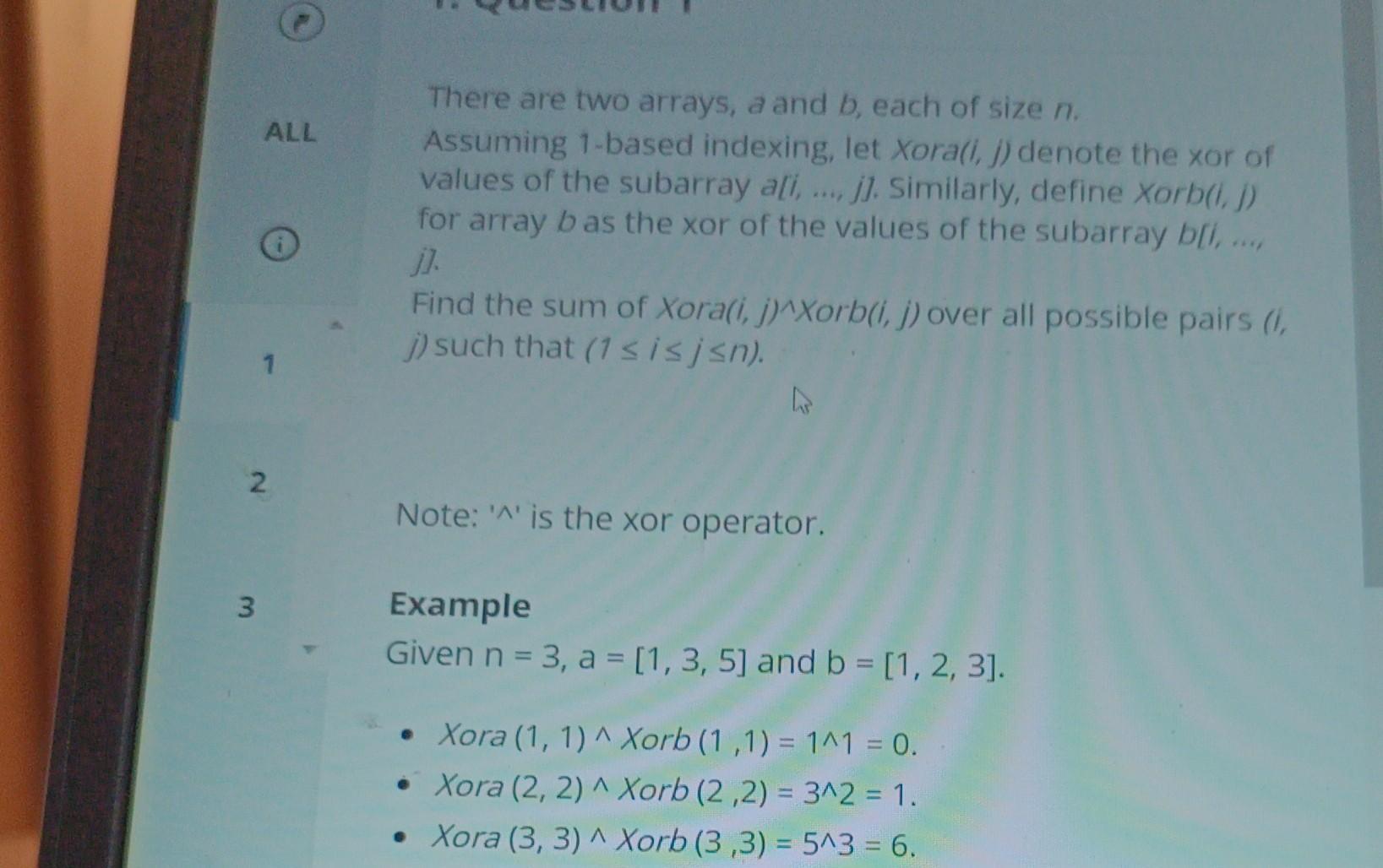
left ALL O 1. Question 1 There are two arrays, a and b, each of size n. Assuming 1-based indexing, let Xora(i, j) denote the xor of values of the subarray a[,...]]. Similarly, define Xorb(i, j) for array b as the xor of the values of the subarray b[i.. Find the sum of Xora(i, j)^Xorb(i, j) over all possible pairs (i j) such that (1 sisjsn). 2 Note: '' is the xor operator. Example Given n = 3, a = [1, 3, 5] and b = [1, 2, 3]. Xora (1, 1)^ Xorb (1,1) = 1^1 = 0. Xora (2, 2) ^ Xorb (2,2) = 3^2 = 1. 9 Xora (3, 3) ^ Xorb (3,3)=5^3 = 6. Xora (1, 2) ^ Xorb (1,2) = (1^3) ^ (1^2) = 2^3 = 1. Xora (2, 3) ^ Xorb (2,3) = (3^5) ^ (2^3) = 6^1 = 7. Xora (1, 3)^ Xorb (1,3) = (1^3^5)^ (1^2^3) = 7^0 = 7. The answer is the sum of the xor values, 0+1+6+1+7+7 = 22. Function Description Complete the function calculateAnswer in the editor below. ALL There are two arrays, a and b, each of size n. Assuming 1-based indexing, let Xora(i, j) denote the xor of values of the subarray a[i,...., j]. Similarly, define Xorb(i, j) for array bas the xor of the values of the subarray b[i,.... j]. Find the sum of Xora(i, j)^Xorb(i, j) over all possible pairs (i, j) such that (1 is jn). E 2 3 Note: '' is the xor operator. Example Given n = 3, a = [1, 3, 5] and b = [1, 2, 3]. Xora (1, 1)^ Xorb (1,1) = 1^1 = 0. Xora (2, 2) ^ Xorb (2,2) = 3^2 = 1. Xora (3, 3) ^ Xorb (3,3) = 5^3 = 6. ALL 1 2 3 22. Function Description Complete the function calculateAnswer in the editor below. calculateAnswer has the following parameter(s): int a[n]: an array of integers int b[n]: an array of integers Returns long the sum of the xor values as described Constraints 1 n 2*105 0 < a[i], b[i] < 108 3 2 Sample Case 0 Sample Input For Custom Testing 17 18 19 STDIN FUNCTION 20 21 223212 a[] size n = 2 22 a = [2, 3] 23 b[] size n = 2 b= [1,2] Sample Output 6 Explanation Xora (1, 1)^ Xorb (1, 1) + Xora (2, 2) ^ Xorb (2, 2) + Xora (1, 2)^ Xorb (1,2) = 2^1+3^2+ ((2^3)^(1^2)) = 3+1+(1^3) = 3+1+2=6 Sample Case 1 Sample Input For Custom Testing STDIN 1 1 1 Sample Output 1 FUNCTION a[] size n = 1 a = [0] b[] size n = 1 b = [1] Explanation Xora (1, 1)^ Xorb (1, 1) = 0^1 = 1 10 /* 111 9012 11 * 12 13 345 * Complete the 'calculateAnswer' function below. * The function is expected to return a LONG_INTEGER. The function accepts following parameters: 14 15 * 1. 16 17 67 18 * */ INTEGER_ARRAY a 2. INTEGER_ARRAY b long calculate Answer (vector a, vector b) { 19 20 21 } 22 23 int main()