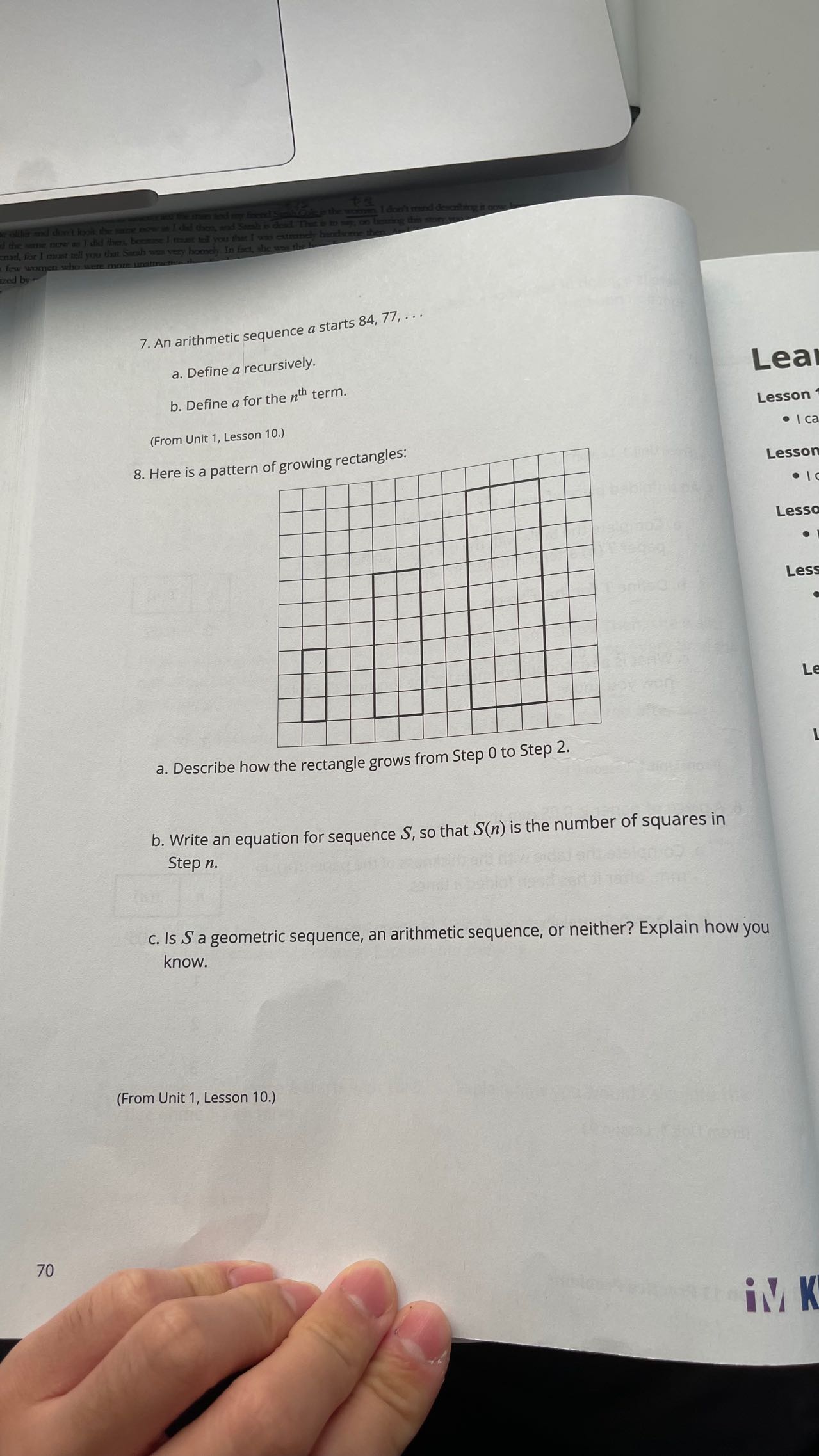
Question: Lesson 11 Practice Problems 4. Here is a graph of sequence r. Define r recursively using 20 1 . Find the sum of the sequence

Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


