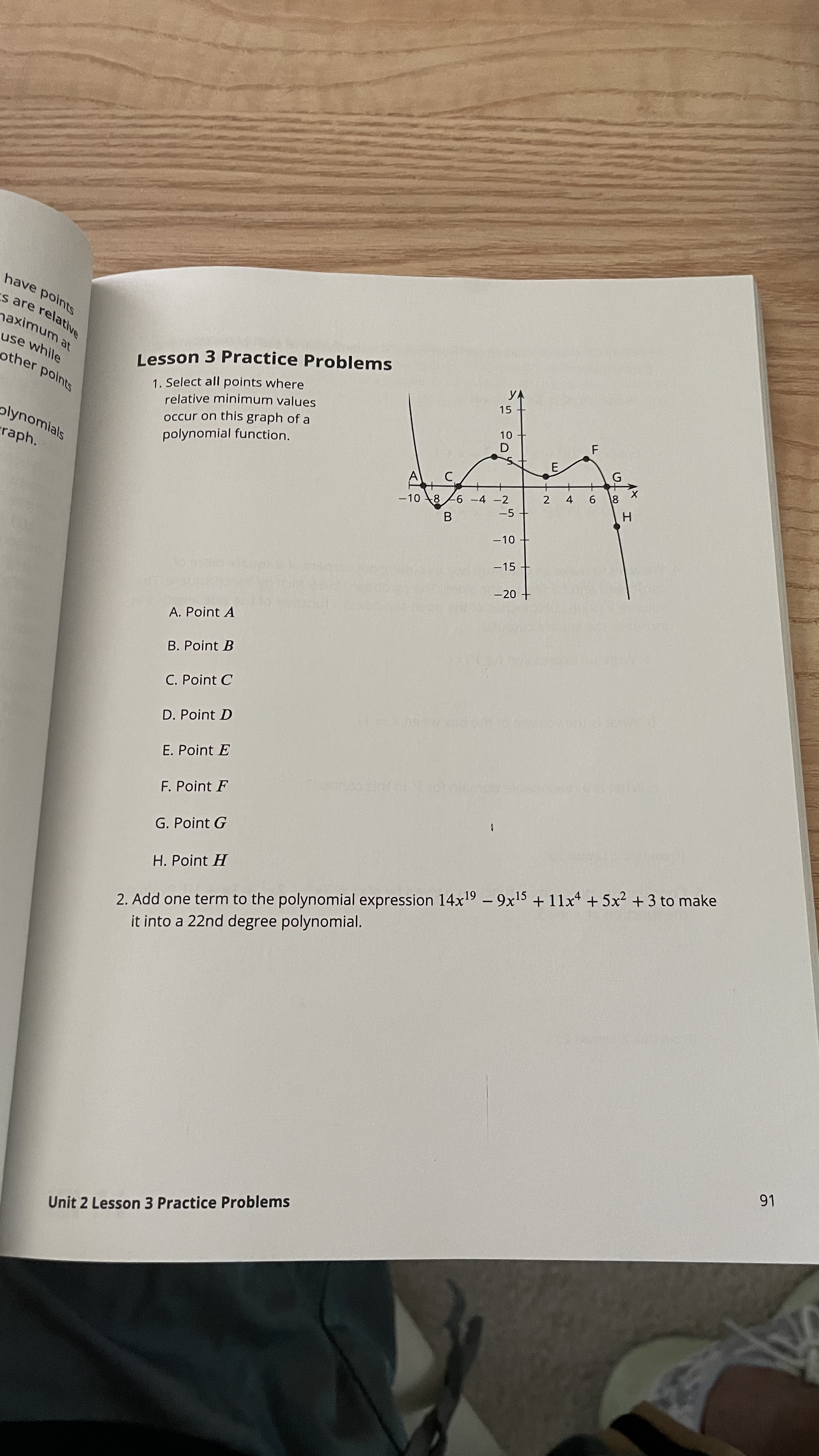
Question: Lesson 2 Practice Problems 1. Select all polynomial expressions that are equivalent to 6x4 + 4x3 __ 7x2 + 5x + 8. A. 16xlo B.



Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


