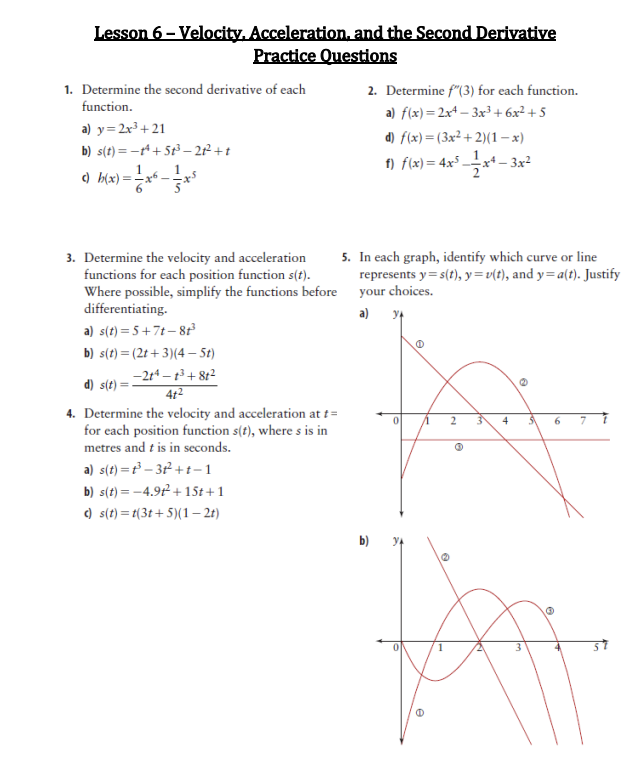
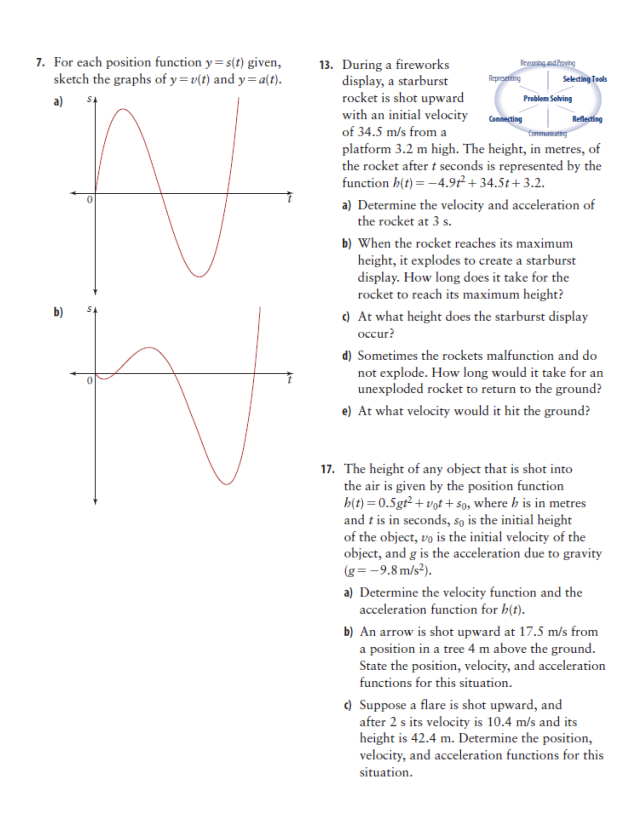
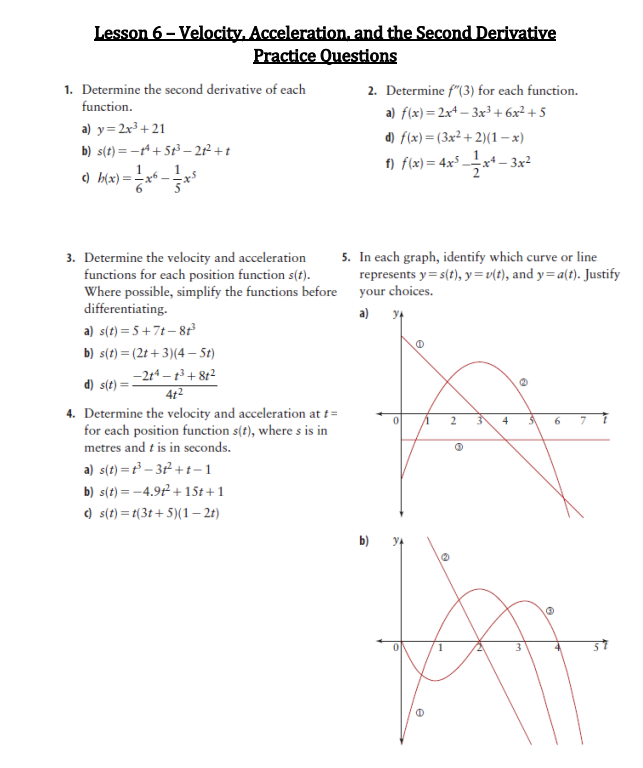
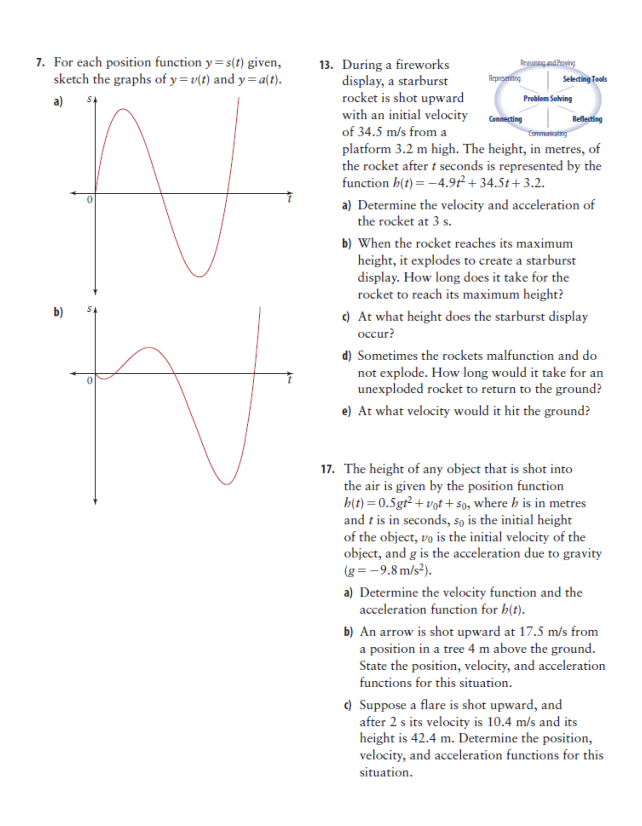
Lesson 6 - Velocity. Acceleration, and the Second Derivative Practice Questions 1. Determine the second derivative of each 2. Determine f"(3) for each function. function. a) f(x) = 2x4 - 3x3+ 6x2+5 a) y= 2x3+21 d) f(x) =(3x2+2)(1 -x) b) s(t ) =-14+ 5+3- 212+1 f) f(x) = 4x5 _-x4 -3x2 ( b(x) =-x6- -x5 3. Determine the velocity and acceleration 5. In each graph, identify which curve or line functions for each position function s(t). represents y = s(t), y = v(f), and y = a(f). Justify Where possible, simplify the functions before your choices. differentiating. a) a) s(t) =5+7t -8+3 b) s(t) = (2+ + 3)(4 - 5t) d) s(t ) = -214-13 + 8+2 4+2 4. Determine the velocity and acceleration at = 0 for each position function s(t), where s is in 2 6 7 metres and f is in seconds. a) s(t) = +3 - 312 +t-1 b) s(t) = -4.9f- + 15t+ 1 () s(t) = *(3t+ 5)(1 - 2t) b)7. For each position function y = s(f) given, 13. During a fireworks Reasoning and Proving sketch the graphs of y = v(t) and y = a(t). display, a starburst Arpreventing Selecting Tools a) rocket is shot upward Problem Solving with an initial velocity anecting Reflecting of 34.5 m/s from a platform 3.2 m high. The height, in metres, of the rocket after t seconds is represented by the function b(t) = -4.912 + 34.5t+ 3.2. a) Determine the velocity and acceleration of the rocket at 3 s. b) When the rocket reaches its maximum height, it explodes to create a starburst display. How long does it take for the rocket to reach its maximum height? b) () At what height does the starburst display occur? d) Sometimes the rockets malfunction and do not explode. How long would it take for an unexploded rocket to return to the ground? e) At what velocity would it hit the ground? 17. The height of any object that is shot into the air is given by the position function b(t) = 0.5gt- + Not + so, where b is in metres and t is in seconds, so is the initial height of the object, vo is the initial velocity of the object, and g is the acceleration due to gravity (g= -9.8 m/s ). a) Determine the velocity function and the acceleration function for b(t). b) An arrow is shot upward at 17.5 m/s from a position in a tree 4 m above the ground. State the position, velocity, and acceleration functions for this situation. () Suppose a flare is shot upward, and after 2 s its velocity is 10.4 m/s and its height is 42.4 m. Determine the position, velocity, and acceleration functions for this situation