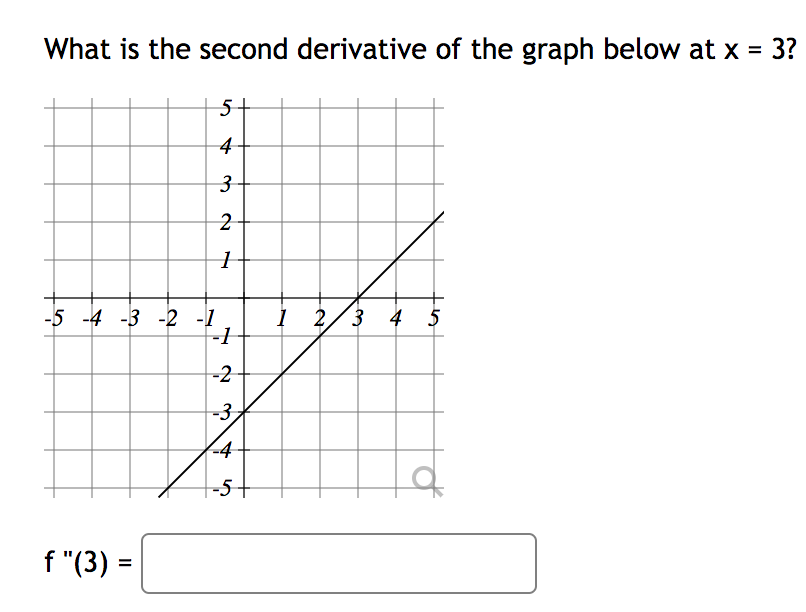
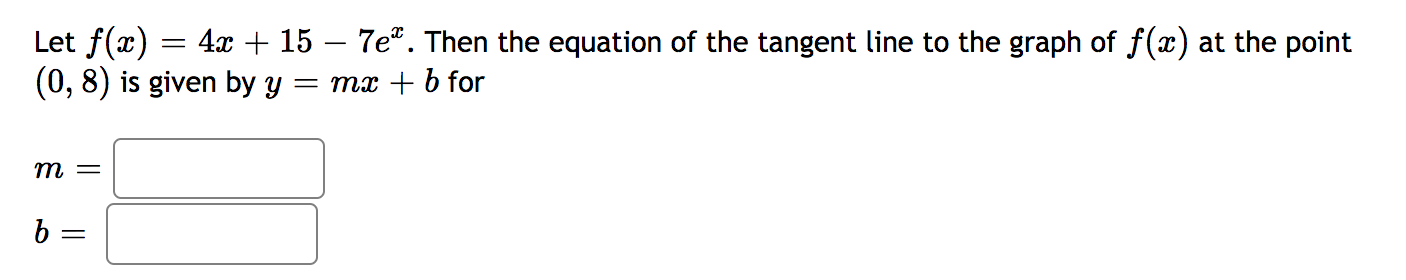
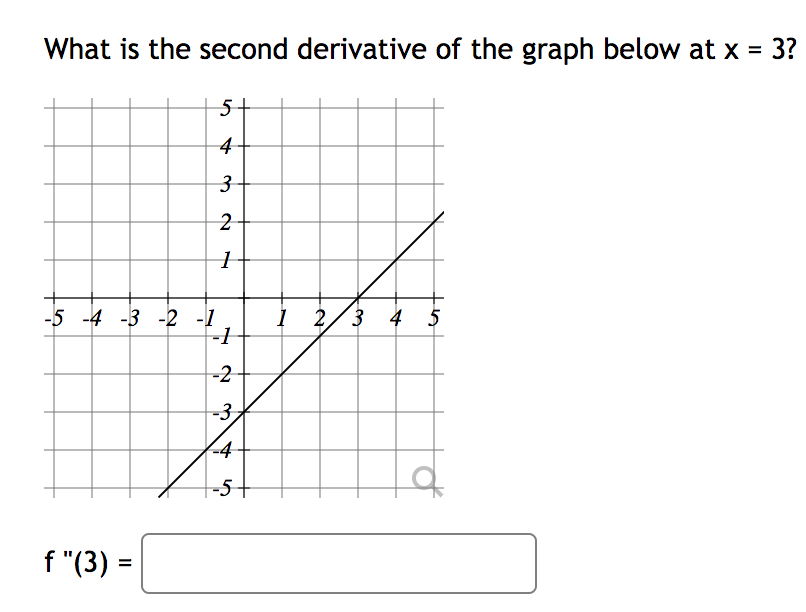
Let 3(t) = 4753 + 6t2 7275 be the equation of motion for a particle. Find a function for the velocity. w) = I:] Where does the velocity equal zero? [Hint: factor out the GCF.] t = C] t = [:1 Find a function for the acceleration of the particle. we: 23mm Let at) 65inm+2cosm' W) = :] The equation of the tangent line to y 2 at) at a = % can be written in the form 3; = mm + b where \fLet at) = 4x + 15 763. Then the equation of the tangent line to the graph of x) at the point (0,8) is given by y = ms: + b for Question Let s(t) = 6 - 3 sin(t) be the height in inches of a mass that is attached to a spring t seconds after it is released. At what height is it released? Initial height inches At what time does the velocity first equal zero? At t = seconds Find a function for the acceleration of the particle. in a(t) = $2What is the second derivative of the graph below at x = 3? -5 -4 -3 -2 -1. 1 2/3 4 UT- f "(3) =