Let A be an integer array with n columns and n rows. The array encodes the map of a room of size n n. We have A[i, j] = 1 if there is a gold coin at location (i, j) in the room, and otherwise A[i, j] = 0. Indiana Jones is initially located at position (1, 1), which is the north-west corner of the room, and has to reach the exit at location (n, n), which is the south-east corner. Indiana Jones is in a hurry, so he can move only south, or east. That is, at each step, starting at location (i, j) he can either move to location (i + 1, j), or (i, j + 1). Note that he cannot move diagonally.

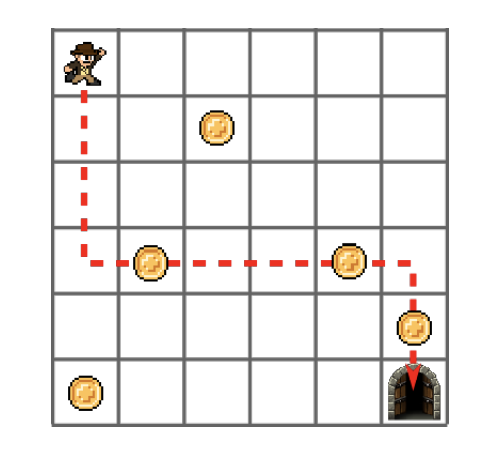
Design an algorithm which, given the array A as input, outputs a sequence of moves for Indiana Jones, that allows him to collect the maximum possible number of gold coins before leaving the room. The running time of your algorithm should be polynomial in n. Hint: Use dynamic programming.

Guidelines for presenting an algorithm as a solution to a problem:

1. Brief, informal, intuitive description. A line or two of English.

2. Detailed description. Mostly English, but may include well-documented pseudocode

and diagrams.

3. Proof of correctness - this means that for all inputs for which this program terminates,

the algorithm gives the correct corresponding output. Sometimes this can be included

in the detailed description if worded appropriately. Usually best to add separately.

Mostly English, math and diagrams.

4. Proof of termination - this means that the algorithm will terminate on all inputs.

Usually trivial, sometimes not. Make sure one way or the other.

5. Analysis of time and space complexity. Upper bound on the worst case is what we

seek in general.